Résolution des équations algébriques de degré 3 et 4

par A. Marrakchi

Galois, dont on fête le bicentenaire cette année, a construit, lors de sa courte vie, l’une des théories mathématiques les plus fécondes et aux domaines d’application les plus larges que l’on connaisse aujourd’hui. En ce qui concerne la théorie des équations, il n’est pas possible de mesurer l’apport réel de Galois sans avoir pris connaissance de ce qui a été fait avant lui. Ce texte propose de montrer quelques aspects de la résolution des équations algébriques de degré 3 et 4 à travers une petite promenade mathématique qui commence au XVIème siècle avec les mathématiciens de la Renaissance italienne et se termine au XVIIIème siècle avec les travaux de Lagrange.

Introduction

Avons d’aborder la résolution des équations proprement dite, il est nécessaire de préciser de quelles équations on parle et ce que l’on entend par « résolution ».

Qu’est-ce qu’une équation algébrique ?

Une équation algébrique (ou polynômiale) est une équation de la forme

$$x^n + a_{n-1} x^{n-1} + \cdots + a_1 x +a_0= 0$$

où l’inconnue est $x$ et où $a_0, a_1, \ldots, a_{n-1}$ sont des nombres connus qu’on appelle coefficients de l’équation. On dit que l’équation est de degré $n$.

Par exemple, les deux équations suivantes sont algébriques, respectivement de degré 2 et 3 :

$$x(x+2)+4=0 \quad ; \quad x^3+3x^2+2x+7=0$$

alors que celle-ci ne l’est pas :

$$x^2-\sin x=0$$

Les mathématiciens se sont très tôt intéressés aux équations algébriques car elles figurent parmi les plus simples que l’on puisse se poser (ce qui ne veut pas dire qu’elles sont faciles à résoudre !) mais aussi parce qu’elles peuvent, lorsque leur degré est plus petit que 3, être reliées à des problèmes concrets faisant intervenir des longueurs, des aires ou des volumes.

Le problème consistant à « résoudre » ce type d’équations peut prendre différentes formes selon les besoins. On peut par exemple chercher à trouver des solutions approchées par des méthodes numériques. Ou bien, chercher à construire géométriquement les solutions comme intersections de certaines courbes dans le plan. Il se trouve que, historiquement, le problème de la résolution de telles équations a acquis, pour les algébristes et donc pour Galois, un sens très précis, celui de la résolution par radicaux.

Résolubilité par radicaux

Essayons de comprendre la notion de résolubilité par radicaux à travers divers exemples. Prenons d’abord une équation de degré 1, par exemple $3x+2=0$. La solution est alors $x=-\frac{2}{3}$. Pour la résoudre nous n’avons pas eu besoin d’autre chose que les quatre opérations de base : $+$,$-$,$\times$ et $\div$.

Si nous essayons de faire la même chose pour l’équation $x^2+2x-1=0$ de degré 2, nous n’y arriverons pas. En effet, les nombres que l’on peut obtenir par les opérations de base à partir des coefficients de l’équation sont des nombres rationnels, c’est-à-dire des nombres qui sont quotients de deux entiers. Or les solutions de cette équation sont $-1+\sqrt{2}$ et $-1-\sqrt{2}$ et les grecs savaient depuis longtemps déjà que $\sqrt{2}$ n’est pas rationnel.

Pour résoudre une équation de degré 2 quelconque de la forme $x^2+2bx+c=0$, on peut procéder comme suit. On remarque que $x^2+2bx$ est le début du développement de $(x+b)^2=x^2+2bx+b^2$. Si on pose $u=x+b$, notre équation se réécrit alors sous la forme (on parle de forme canonique) $u^2-b^2+c=0$ et la condition $u=x+b$ devient $x=u-b$. Nous avons donc le système suivant

$$\left\{\begin{array}{l}
u^2=b^2-c \\
x=u-b
\end{array}\right.$$

Remarquons que pour trouver une expression de $x$, il suffit alors d’écrire que $u=\pm \sqrt{b^2-c}$ puis d’utiliser $x=-b+u$.

Regardons enfin l’équation suivante :

$$(x^3-1)^8+2b(x^3-1)^4+c=0$$

Si on pose $v=x^3-1$, alors on remarque que $v^8+2bv^4+c=0$ c’est-à-dire que $v^4$ vérifie l’équation $y^2 + 2by + c = 0$ que l’on a résolu tout à l’heure. On sait alors qu’on a un système de la forme

$$\left\{\begin{array}{l}
u^2=b^2-c \\
v^4=u-b
\end{array}\right.$$

Puis, comme $x^3=v+1$, on obtient finalement le système suivant

$$\left\{\begin{array}{l}
u^2=b^2-c \\
v^4=u-b \\
x^3=v+1.
\end{array}\right.$$

Encore une fois, on peut donner une expression de $x$ en utilisant les fonctions $\sqrt{\cdot}$, $\sqrt[3]{\cdot}$ et $\sqrt[4]{\cdot}$

En conclusion, pour chacune des équations précédentes nous avons réussi à écrire un système de la forme

$$\left\{\begin{array}{l}
u_1^{p_1}=\cdots\\
u_2^{p_2}=\cdots\\
\vdots \\
u_r^{p_r}=\cdots
\end{array}\right.$$

avec $u_r=x$ et où, à chaque fois, le membre de droite s’exprime avec les quatre opérations de base à partir des coefficients de l’équation et des inconnues $u_i$ précédentes.

Lorsqu’on arrive à montrer que les solutions d’une équation algébrique vérifient un système de cette forme, on dit que l’équation est résoluble par radicaux. Le terme « radicaux » vient du fait que l’on peut obtenir une expression de la solution $u_r=x$ en écrivant à chaque étape $i$ que $u_i$ est une racine $p_i$-ieme du second membre. On obtient au final une expression de $x$ à partir des coefficients de l’équation initiale qui n’utilise que les opérations de base et les fonctions $\sqrt[n]{\cdot}$ : une expression par radicaux. Par exemple,

$$\frac{\sqrt[3]{1+\sqrt{2}}+\sqrt[3]{-1+\sqrt{2}}}{5}.$$

Équation du troisième degré et quatrième degré

Comme nous l’avons plus haut, toutes les équations de degré 1 et 2 sont résolubles par radicaux. Les babyloniens savaient résoudre ces équations depuis déjà 4000 ans. Il aura fallu attendre la Renaissance italienne pour que d’autres progrès significatifs se fassent dans ce domaine : d’abord la résolution (par radicaux) de l’équation du troisième degré grâce aux formules de Tartaglia-Cardan, puis peu de temps après, celle de l’équation du quatrième degré grâce à la méthode de Ferrari.

Équation du troisième degré : méthode de Cardan

La première méthode connue pour résoudre une équation du troisième degré fut donnée par l’italien Jérôme Cardan. En fait, cette méthode lui aurait été confiée par un autre mathématicien italien connu sous le nom de Tartaglia. Après avoir d’abord promis de la garder secrète, Cardan finit par la publier en 1545 à la grande surprise de Tartaglia ! Voici cette méthode.

On cherche à résoudre l’équation $x^3+px+q=0$. Nous verrons plus loin pourquoi on ne s’intéresse qu’aux équations qui sont de cette forme. L’idée de la méthode de Cardan consiste à chercher $x$ sous le forme $x=u+v$ et de chercher à poser une condition sur $u$ et $v$ a posteriori afin d’obtenir une équation plus simple à résoudre. En remplaçant dans l’équation on obtient $(u+v)^3+p(u+v)+q=0$ puis, en développant et en réarrangeant les termes, il vient $u^3+v^3+(3uv+p)(u+v)+q=0$. En vue de simplifier l’équation, la condition sur $u$ et $v$ que l’on va imposer est $3uv+p=0$. L’équation devient alors $u^3+v^3=-q$ et la condition sur $u$ et $v$ se réécrit $uv=-\frac{p}{3}$. On obtient donc le système suivant

$$\left\{\begin{array}{l}
u^3+v^3 = -q \\
u^3v^3 = -\left( \frac{p}{3} \right)^3
\end{array}\right.$$

Or, si on connait la somme et le produit de deux nombres, ici $u^3$ et $v^3$, on peut trouver ces nombres comme solutions d’une équation du second degré ! En effet,

$$(X-u^3)(X-v^3)=X^2-(u^3+v^3)X+u^3v^3=X^2+qX-\left( \frac{p}{3} \right)^3$$

Ainsi, $u^3$ et $v^3$ sont les solutions de l’équation $X^2+qX-( \frac{p}{3} )^3 = 0$. Comme on sait résoudre cette équation par radicaux, on sait que $u^3$ et $v^3$ sont exprimables par radicaux à partir des coefficients $q$ et $( \frac{p}{3} )^3$, et donc à partir des coefficients $p$ et $q$ de l’équation initiale. Finalement, comme $x=u+v$, $x$ est exprimable par radicaux à partir de $p$ et $q$. On en déduit

Proposition. L’équation de degré 3, $x^3+px+q=0$, est résoluble par radicaux.
Une solution générique possible est donnée par

$$x=\sqrt[3]{\frac{-q+\sqrt{q^2+4 \left( \frac{p}{3}
\right)^3}}{2}}+\sqrt[3]{\frac{-q-\sqrt{q^2+4 \left( \frac{p}{3}
\right)^3}}{2}}.$$

Remarque 1 : Expliquons maintenant pourquoi nous nous sommes contentés de résoudre des équations du troisième degré du type $x^3+px+q=0$. En fait, la raison est que toute équation du troisième degré peut se mettre sous cette forme. En effet, si l’on a une équation de la forme $x^3+ax^2+bx+c=0$. Alors, en opérant le changement de variable $x=y-\frac{a}{3}$, le terme $x^3=(y-\frac{a}{3})^3$ se développe en $y^3-ay^2+\cdots$ et le terme $ax^2=a(y-\frac{a}{3})^2$ se développe en $ay^2+\cdots$. On voit que les deux termes $-ay^2$ et $ay^2$ se simplifient et il reste une équation en $y$ de la forme $y^3+py+q=0$ que l’on sait résoudre. On retrouve ensuite $x$ avec la relation $x=y-\frac{a}{3}$.

Remarque 2 : La méthode de Cardan pose, dans certains cas, quelques difficultés. Par exemple, si l’on cherche à résoudre l’équation $x^3-15x-4=0$. Alors l’équation du second degré intermédiaire qu’il faut résoudre est $X^2-4X+125=0$ qui n’admet pas de solutions (son discriminant est négatif). Pourtant l’équation initiale admet bien une solution : $x=4$ ! Bombelli eut alors le premier l’idée d’appliquer formellement la formule générique donnée plus haut, ce qui l’oblige à considérer une racine carré d’un nombre négatif ! Il effectue alors les calculs sur ce nombre imaginaire avec les règles habituelles et trouve à la fin la solution recherchée $x=4$. Ce fut la naissance des nombres complexes : des nombres de la forme $x+\sqrt{-1}\:y$ où $x$ et $y$ sont des nombres réels et $\sqrt{-1}$ est un nombre imaginaire vérifiant $(\sqrt{-1})^2=-1$ !

Équation du quatrième degré : méthode de Ferrari

L’équation du 4^ème degré fut résolue en 1540 par Ferrari à l’âge de 18 ans. Sa solution repose sur la méthode de Cardan dont il était d’ailleurs l’élève.

On cherche à résoudre l’équation $x^4=px^2+qx+r$. Comme pour l’équation de degré 3, un changement de variable permet de ramener toute équation du quatrième degré à une équation de cette forme-là.

L’idée de Ferrari consiste à rajouter un paramètre supplémentaire $t$ en écrivant que $x^4=(x^2+t)^2-2x^2t-t^2$. On obtient alors $(x^2+t)^2-2x^2t-t^2=px^2+qx+r$ ou encore $(x^2+t)^2=(2t+p)x^2+qx+(t^2+r)$.

On choisit alors une valeur de $t$ convenable de telle sorte que la quantité $(2t+p)x^2+qx+(t^2+r)$ se factorise sous la forme $(\alpha x +\beta)^2$. Or, dire que $ax^2+bx+c$ se factorise sous la forme $(\alpha x +\beta)^2$ revient à dire que son discriminant $b^2-4ac$ est nul. Dans notre cas, la condition sur $t$ est donc $q^2-4(2t+p)(t^2+r)=0$. Ceci donne lieu à une équation du troisième degré en $t$. Pour la résoudre, Ferrari utilise la méthode de Cardan. Il trouve alors $t$ puis calcule $\alpha$ et $\beta$ et obtient finalement $(x^2+t)^2=(\alpha x +\beta)^2$ où $\alpha$ et $\beta$ sont exprimés par radicaux en fonction de $p$, $q$ et $r$.

Comme $A^2=B^2$ équivaut à $A=\pm B$, on en déduit que $x$ vérifie l’une des deux équations suivantes

$$\left\{\begin{array}{l}
x^2+t=\alpha x +\beta \\
x^2+t=-\alpha x -\beta
\end{array}\right.$$

Toutes deux sont des équations de degré 2 que l’on sait résoudre par radicaux. On en déduit

Proposition. L’équation de degré 4,$ x^4=px^2+qx+r$ est résoluble par radicaux.

Fonctions symétriques et méthode de Lagrange

La résolution des équations du troisième et quatrième degré donna un élan considérable à l’algèbre au cours des siècles qui suivirent. Pourtant, malgré tous les efforts déployés par les mathématiciens, il a fallu attendre près de 300 ans pour qu’Abel puis Galois apportent enfin la réponse (négative !) à la question de la résolubilité par radicaux des équations de degré supérieur. Entre temps, des progrès important furent accomplis incluant l’apparition des notations algébriques modernes et l’utilisation systématique des nombres négatifs, voire complexes.

Une propriété importante fut découverte (quoique la preuve, apportée par Gauss, tarda à venir) : toute équation de degré $n$ admet exactement $n$ solutions dans l’ensemble des nombres complexes. On peut alors toujours mettre une équation

$$x^n + a_{n-1} x^{n-1} + \cdots + a_1 x +a_0= 0$$

sous la forme

$$(x-r_1)(x-r_2)\cdots(x-r_n)=0$$

où les $r_i$ sont les nombres complexes solutions de l’équation qu’on appellera les racines du polynôme $P(x)=x^n + a_{n-1} x^{n-1} + \cdots + a_1 x +a_0$. Notons que les $r_i$ ne sont pas forcément distincts, dans ce cas on parle de racines multiples.

On remarque alors des identités reliant les racines $x_i$ aux coefficients $a_i$. En effet, si l’on met par exemple un polynôme du second degré $x^2+bx+c$ sous la forme $(x-r_1)(x-r_2)$, on trouve en développant $x^2+bx+c=x^2-(r_1+r_2)x+r_1r_2$ d’où

$$\left\{\begin{array}{l}
r_1+r_2=-b \\
r_1r_2=c
\end{array}\right.$$

Nous avons d’ailleurs déjà utilisé ces relations pour la méthode Cardan afin de calculer $u^3$ et $v^3$.

De même, pour un polynôme de degré 3, on écrit $x^3+bx^2+cx+d=(x-r_1)(x-r_2)(x-r_3)$ et on obtient

$$\left\{\begin{array}{l}
r_1+r_2+r_3=-b \\
r_1r_2+r_2r_3+r_1r_3=c\\
r_1r_2r_3=-d
\end{array}\right.$$

On a des relations similaires quelque soit le degré $n$. On les appelle relations coefficients-racines.

Il est intéressant de noter que les expressions $r_1+r_2+r_3$, $r_1r_2+r_2r_3+r_1r_3$, $r_1r_2r_3$ sont symétriques en les racines. Cela signifie que si l’on permute les racines entre elles, alors ces quantités restent inchangées. Par exemple, $(r_1+r_2)r_3^2+(r_1+r_3)r_2^2+(r_2+r_3)r_1^2$ est aussi symétrique, alors que $(r_1-r_2)(r_1-r_3)(r_2-r_3)$ n’est pas symétrique car si l’on échange $r_2$ et $r_3$, l’expression se transforme en son opposée.

Les coefficients d’un polynôme s’expriment ainsi comme des fonctions symétriques des racines. Il en est, par suite, de même de toutes les quantités que l’on peut former en additionnant et/ou en multipliant ces coefficients.

Newton fit alors une découverte remarquable : si, réciproquement, on considère une quantité qui est fonction symétrique des racines d’un polynôme, alors celle-ci peut être exprimée en fonction des coefficients de ce polynôme par sommes et produits. Par exemple, toujours dans le cas du polynôme de degré 3, prenons la quantité symétrique $r_1^3 + r_2^3 + r_3^3$. Un peu de calcul montre que l’on a alors :

$$\begin{array}{l}
r_1^3 + r_2^3 + r_3^3 \\
\hspace{0.5cm} = (r_1+r_2+r_3)^3 – 3(r_1r_2^2 + r_2r_1^2 + r_1r_3^2 + r_3r_1^2 + r_2r_3^2 + r_3r_2^2) – 6r_1r_2r_3 \\
\hspace{0.5cm} = (r_1+r_2+r_3)^3 – 3(r_1+r_2+r_3)(r_1r_2+r_2r_3+r_1r_3)+3r_1r_2r_3
\end{array}$$

Donc d’après les relations coefficients-racines données plus haut, on a $r_1^3 + r_2^3 + r_3^3=-b^3+3bc-3d$. Ainsi, la quantité $r_1^3 + r_2^3 + r_3^3$, et plus généralement, toute quantité qui est symétrique en les racines, peut être exprimée directement à l’aide des coefficients du polynôme sans avoir à trouver les racines au préalable ! Ce théorème fondamental, que l’on admettra ici, est d’une importance capitale et constitue la pierre fondatrice de la théorie de Galois. C’est aussi le point de départ des travaux de Lagrange.

La méthode de Lagrange

Les idées de Lagrange peuvent être considérées comme les prémices de la théorie de Galois. Galois trouva d’ailleurs certainement son inspiration en lisant les écrits de Lagrange : son mémoire Réflexions sur la résolution algébrique publié en 1771 ou, plus probablement, une note sur ce mémoire qu’il aurait écrit plus tard. Lagrange développe une réflexion générale sur la résolution des équations en étudiant comment se transforment certaines quantités exprimées en fonctions des racines d’un polynôme lorsqu’on permute ces racines. Grâce à cela, Lagrange donne une méthode très générale de résolution des équations qui permet notamment d’unifier les méthodes connues de résolution des équations du troisième et quatrième degré. C’est ce que nous allons voir.

Lagrange fait la remarque suivante : lorsqu’on cherche à résoudre une équation dont les racines sont $r_1, r_2, \ldots,r_n$ et que l’on forme une certaine quantité $t$ en fonction de ces racines $t=f(r_1,r_2,\ldots,r_n)$ alors $t$ est très facile à calculer en fonctions des coefficients de l’équation lorsque, d’après la propriété vue plus haut, $f$ est symétrique en les racines $r_i$. Dans ce cas, lorsqu’on permute les racines $r_i$ entre elles, l’expression $t=f(r_1,r_2,\ldots,r_n)$ garde une valeur constante. Parallèlement, lorsque $f$ est très peu symétrique, par exemple lorsque $t=r_1-r_3$, alors $t$ peut être très difficile à calculer. Cette fois, lorsqu’on permute les racines $r_i$, $t$ peut potentiellement prendre de nombreuses valeurs différentes. Par exemple, pour $n=3$, $t$ peut prendre les valeurs $r_1-r_3$, $r_2-r_3$, $r_1-r_2$, $r_2-r_1$, $r_3-r_1$ et $r_3-r_2$.

Nous avons peu d’espoir d’arriver à calculer directement une quantité $t$ peu symétrique (typiquement lorsque $t$ est une racine) et calculer des quantités totalement symétriques est certes facile, mais ne fait pas vraiment avancer le problème. L’idée de Lagrange est d’essayer de former une quantité qui soit à la fois assez symétrique, dans l’espoir qu’elle ne prenne qu’un nombre petit de valeurs et donc qu’elle soit assez facilement calculable, et à la fois pas trop symétrique, dans l’espoir que les racines pourront être exprimées à partir de cette quantité. De telles quantités sont appelées des résolvantes de Lagrange. Regardons tout de suite comment s’articule ce principe avec l’équation de degré 3.

Équation du troisième degré

On cherche à résoudre une équation de degré 3 dont les racines (pour l’instant inconnues) sont $r_1$, $r_2$ et $r_3$. En vue de résoudre l’équation, la quantité intermédiaire que l’on va considérer est $u=r_1+jr_2+j^2r_3$ où $j$ est un nombre complexe différent de 1 vérifiant $j^3=1$ (un tel nombre existe car l’équation $x^3=1$ admet trois solutions dans l’ensemble des nombres complexes, dont deux sont différentes de $1$).

Première étape

Quelles sont les valeurs que prend $u$ lorsqu’on permute les racines $r_1$, $r_2$ et $r_3$ ? Représentons $r_1$, $r_2$ et $r_3$ par les sommets $A$,$B$ et $C$ d’un triangle équilatéral. Permuter les racines $r_1$,$r_2$ et $r_3$ revient alors à appliquer une isométrie au triangle $ABC$. Ces isométries sont soit des rotations (d’angle $0°$, $120°$, ou $-120°$), soit des symétries d’axe l’une des médiatrices du triangle. Commençons par les rotations. La rotation qui envoie $A$ sur $B$, $B$ sur $C$ et $C$ sur $A$ peut être représentée par le tableau

$$\begin{pmatrix}
A&B&C\\
B&C&A
\end{pmatrix}$$

où la deuxième ligne indique les images des points de la première ligne. Les trois rotations sont donc données par

$$\begin{pmatrix}
A&B&C\\
A&B&C
\end{pmatrix} \quad \begin{pmatrix}
A&B&C\\
B&C&A
\end{pmatrix}
\quad \begin{pmatrix}
A&B&C\\
C&A&B
\end{pmatrix}$$

Les valeurs respectives que prend $u$ sont alors

$$\left\{\begin{array}{l}
u = r_1 + jr_2 + j^2r_3 \\
u’ = r_2 + jr_3 + j^2r_1 \\
u” = r_3 + jr_1 + j^2r_2 \\
\end{array}\right.$$

On remarque alors que $u=ju’=j^2u”$ grâce à la relation $j^3=1$ ! Donc si on élève au cube, on a $u^3=u’^3=u”^3$. Ainsi, effectuer une rotation des racines laisse la quantité $u^3$ invariante !

Maintenant, regardons les symétries axiales. Elles sont décrites par les tableaux suivants

$$\begin{pmatrix}
A&B&C\\
A&C&B
\end{pmatrix} \quad \begin{pmatrix}
A&B&C\\
C&B&A
\end{pmatrix}
\quad \begin{pmatrix}
A&B&C\\
B&A&C
\end{pmatrix}$$

Par ces transformations, $u$ prend encore trois valeurs qui sont $v=r_1+jr_3+j^2r_2$, $v’=r_3+jr_2+j^2r_1$ et $v”=r_2+jr_1+j^2r_3$. Encore une fois, on remarque que $v^3=v’^3=v”^3$. Ainsi, lorsqu’on applique une symétrie axiale quelconque à $u^3$ alors $u^3$ se transforme en $v^3$.

En conclusion, $u^3$ est inchangée par les rotations et se transforme en $v^3$ par les symétries axiales. Donc, finalement lorsqu’on effectue une permutation quelconque des racines, $u^3$ ne prend que les deux valeurs $u^3=(r_1+jr_2+j^2r_3)^3$ et $v^3=(r_1+jr_3+j^2r_2)^3$. Ceci va nous permettre d’exprimer $u^3$ et $v^3$ à partir des coefficients de l’équation initiale. En effet, les deux quantités $S=u^3+v^3$ et $P=u^3v^3$ sont totalement symétriques en les racines car appliquer une permutation des racines ne fait qu’échanger $u^3$ et $v^3$. Par conséquent, d’après la propriété fondamentale que l’on a vue plus haut, $S$ et $P$ peuvent être exprimées directement en fonction des coefficients de l’équation de départ sans avoir à calculer les racines au préalable. Mais une fois $S$ et $P$ connues, on a à faire à un système somme-produit, d’où on trouve que $u^3$ et $v^3$ sont solutions de l’équation du second degré $y^2-Sy+P=0$. Ceci permet donc d’affirmer que $u^3$ et $v^3$ sont exprimables par radicaux à partir des coefficients de l’équation initiale ! C’est la première étape.

Deuxième étape

Maintenant que l’on connait $u^3$ et $v^3$, il faut pouvoir retrouver les racines ! Pour cela, on va utiliser l’identité $1+j+j^2=0$. Elle est bien vraie car de $j^3=1$, on déduit $j^3-1=(j-1)(1+j+j^2) = 0$ puis $1+j+j^2 = 0$ étant donné que $j \neq 1$. Maintenant, rappelons que $u=r_1+jr_2+j^2r_3$, $v=r_1+jr_3+j^2r_2$. De plus, la somme $\sigma = r_1+r_2+r_3$ est symétrique en les racines donc connue. On a alors le système

$$\left\{\begin{array}{l}
\sigma = r_1+r_2+r_3 \\
u = r_1+jr_2+j^2r_3 \\
v = r_1+jr_3+j^2r_2
\end{array}\right.$$

En sommant membre à membre, on obtient

$$\sigma + u + v = 3r_1+(1+j+j^2)r_2+(1+j+j^2)r_3=3r_1$$

d’où $r_1=\frac{\sigma + u + v }{3}$. De même, $r_2=\frac{\sigma + u’ + v” }{3}=\frac{\sigma + j^2u + jv }{3}$ et $r_3 = \frac{\sigma + u” + v’ }{3} = \frac{\sigma + ju + j^2v }{3}$. Nous avons bien réussi à exprimer les solutions de l’équation à l’aide de $u$ et $v$. Comme $u^3$ et $v^3$ sont exprimables par radicaux à partir des coefficients de l’équation initiale, alors les racines aussi.

Remarquons que comme pour la méthode Cardan, la résolution de l’équation a nécessité la résolution d’une équation du second degré intermédiaire puis l’extraction de deux racines cubiques à partir de $u^3$ et $v^3$. Les méthodes sont fondamentalement identiques mais comme nous allons le voir, l’idée de Lagrange s’adapte pour l’équation de degré 4.

Équation du quatrième degré

Le principe est le même. On cherche à résoudre une équation dont les racines sont $r_1$, $r_2$, $r_3$ et $r_4$. Cette fois-ci, la quantité que l’on va former est $x=r_1 r_2 + r_3 r_4$.

Première étape

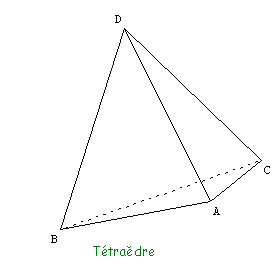
Quelles sont les valeurs prises par $x$ lorsqu’on permute les racines $r_1$, $r_2$, $r_3$ et $r_4$ ? Cette fois-ci, on peut représenter chaque permutation des racines par une isométrie d’un tétraèdre régulier de sommets $A$, $B$, $C$ et $D$. Le tétraèdre $ABCD$ possède trois paires d’arêtes opposées : $\{AB,CD\}$, $\{AC,BD\}$ et $\{AD,BC\}$. En outre, chaque isométrie du tétraèdre transforme une paire d’arêtes opposées en une autre. Par exemple l’isométrie

$$\begin{pmatrix}
A&B&C&D\\
B&C&D&A
\end{pmatrix}$$

transforme $\{AB,CD\}$ en $\{AD,BC\}$ et laisse $\{AC,BD\}$ inchangée. Si l’on fait correspondre au point $A$ la racine $r_1$, au point $B$ la racine $r_2$, etc., à l’arête $AB$ le produit $r_1 r_2$, etc. et à la paire d’arête $\{AB,CD\}$ la quantité $r_1 r_2 + r_3 r_4$, etc., on déduit de ce qui précède que toute permutation des racines des racines transforme la quantité $x=r_1 r_2 + r_3 r_4$ en l’une des quantités suivantes (qui correspondent aux trois paires d’arêtes) : $x=r_1 r_2 + r_3 r_4$, $y=r_1 r_3 + r_2 r_4$ ou $z=r_1 r_4 + r_2 r_3$. Comme pour le cas du degré 3, on en déduit que les trois quantités $S=x+y+z$, $T=xy+yz+xz$ et $P=xyz$ sont symétriques. Elle sont donc connues, et on peut déterminer $x$, $y$ et $z$ comme solutions de l’équation du troisième degré $X^3-SX^2+TX-P=0$.

Deuxième étape

Il s’agit maintenant de trouver les racines $r_1$, $r_2$, $r_3$ et $r_4$, connaissant les quantités $x=r_1 r_2 + r_3 r_4$, $y=r_1 r_3 + r_2 r_4$ et $z= r_1 r_4 + r_2 r_3$. Pour cela, posons $p_{12}=r_1 r_2$ et $p_{34}=r_3 r_4$. On a alors $p_{12}+p_{34}=x$ mais il se trouve aussi que $p=p_{12}p_{34}=r_1r_2r_3r_4$ est symétrique en les racines. Donc $p$ est connue et, par conséquent, on aboutit encore une fois à un système somme-produit :

$$\left\{\begin{array}{l}
x = p_{12}+p_{34} \\
p = p_{12}p_{34}\\
\end{array}\right.$$

duquel on déduit les valeurs de $p_{12}$ et $p_{34}$ en résolvant une équation de degré 2. Notons maintenant $s_{12}=r_1 + r_2$ et $s_{34}=r_3+ r_4$. Alors $s=s_{12}+s_{34}=r_1+r_2+r_3+ r_4$ est symétrique donc connue. Et

$$\begin{array}{rcl}
g&=&p_{34}s_{12}+p_{12}s_{34}\\
&=&r_3r_4(r_1+r_2)+r_1r_2(r_3+r_4)\\
&=&r_1r_2r_3+r_1r_2r_4+r_1r_3r_4+r_2r_3r_4
\end{array}$$

est aussi symétrique donc connue. Les deux inconnues $s_{12}$ et $s_{34}$ vérifient donc le système suivant

$$\left\{\begin{array}{rrrcl}
s_{12}&+&s_{34}&=&s \\
p_{34}s_{12}&+&p_{12}s_{34}&=&g\\
\end{array}\right.$$

qui est un système linéaire (on rappelle que $p_{12}$ et $p_{34}$ ont déjà été déterminées plus haut). On peut facilement le résoudre, par exemple en écrivant $s_{34}=s-s_{12}$ et en remplaçant dans la deuxième équation pour avoir une équation du premier degré en $s_{12}$. Après avoir calculé $s_{12}$, on retrouve $s_{34}$ avec $s_{34}=s-s_{12}$. Nous y sommes presque ! On connait $s_{12}$ et $p_{12}$, c’est-à-dire la somme et le produit de $r_1$ et $r_2$ ! Donc en résolvant une deuxième équation du second degré, on peut trouver $r_1$ et $r_2$. Enfin, pour trouver $r_3$ et $r_4$, on peut remarquer qu’ils sont solutions du système linéaire suivant

$$\left\{\begin{array}{rrrcl}
r_3&+&r_4&=&s_{34} \\
r_1r_3&+&r_2r_4&=&y\\
\end{array}\right.$$

Nous avons bel et bien montré que l’équation de degré 4 est résoluble par radicaux.

On remarque encore une fois que la méthode de Lagrange possède beaucoup de points communs avec celle de Ferrari. En particulier, dans chacune des deux méthodes, nous avons dû calculer une quantité intermédiaire en résolvant une équation du troisième degré ce qui nous permettait ensuite de trouver les 4 racines de l’équation initiale en résolvant deux autres équations du second degré. Les résultats de la théorie de Galois montrent, en fait, qu’on ne peut y échapper quelque soit la méthode utilisée.

Lagrange ne s’arrète pas là et sa méthode permet même de résoudre des équations de degré plus grand que 4 mais dans des cas très particuliers. Il pressent que les équations de degré supérieur ne sont pas résolubles en général et développe même quelques arguments en faveur de cette hypothèse. C’est Abel et Galois qui, s’appuyant tous les deux sur les travaux de Lagrange, finiront par montrer indépendamment l’un de l’autre que l’équation de degré 5 n’est pas résoluble par radicaux. Galois va plus loin et répond complètement à la question de la résolubilité en donnant une condition nécessaire et suffisante pour qu’une équation soit résoluble par radicaux.

Conclusion : vers la théorie de Galois

On peut au moins retenir deux choses de ce qui a été fait. D’abord que les équations de degré plus petit que 4 sont résolubles. Puis que dans cette résolution, les permutations des racines jouent un rôle central mais mystérieux. Alors que Lagrange ne raisonnait sur l’action de ses permutation sur les racines d’une équation, Galois considère l’ensemble des permutations de $n$ éléments (en l’occurrence $n$ racines) comme un objet mathématique à part entière dont on peut étudier les propriétés et la structure. Cette structure prend, grâce à Galois, le nom de groupe. Galois montre alors que chaque propriété d’une équation se traduit par une propriété du groupe correspondant (groupe de Galois) et vice versa. Cette démarche lui permet alors de formuler un critère de résolubilité d’une équation à l’aide de son groupe de Galois !