Représentations galoisiennes et théorème de Fermat-Wiles

par B. Edixhoven

L’auteur remercie X. Caruso d’avoir agrandi l’accessibilité du texte initial par une simplification du vocabulaire et l’ajout de plusieurs passages explicatifs.

Le but de ce texte est d’expliquer, à des étudiants de mathématiques dès la deuxième année, ce que sont les représentations galoisiennes qui jouent un rôle si important dans la preuve par Wiles du théorème de Fermat.
Prérequis : un peu de langage des mathématiques (ensembles, fonctions), nombres complexes. Le niveau montera un peu, au fur et à mesure.

Automorphismes des nombres complexes

Notre point de départ est l’ensemble $\mathbb C$ des nombres complexes. Rappelons que chaque nombre complexe s’écrit de façon unique comme $a+bi$ avec $a$ et $b$ des nombres réels, c’est-à-dire, $a$ et $b$ sont dans $\mathbb R$. L’addition dans $\mathbb C$ se fait coordonnée par coordonnée :

$$(a+bi)+(c+di) = (a+c) + (b+d)i,$$

tandis que la multiplication se déduit de la relation $i^2=-1$ :

$$(a+bi)\cdot (c+di) = (ac-bd) + (ad+bc)i.$$

Dans $\mathbb C$ on peut aussi diviser (sauf par $0$ bien sûr) :

$$\frac{1}{a+bi} = \frac{a-bi}{(a+bi)(a-bi)} = \frac{a-bi}{a^2+b^2}
= \frac{a}{a^2+b²}+\frac{-b}{a^2+b²}i.$$

Pour la notion de symétrie en théorie des nombres, qui est à la base de la théorie de Galois, nous n’allons pas considérer la distance sur $\mathbb C$ mais les propriétés algébriques : l’addition et la multiplication. Les symétries de $\mathbb C$ s’appellent alors des automorphismes et sont définis comme suit.

Définition. Les automorphismes de $\mathbb C$ sont les applications $\sigma\colon\mathbb C\to\mathbb C$ qui satisfont à :

• $\sigma(z+w)=\sigma(z)+\sigma(w)$,
• $\sigma(z{\cdot}w)=\sigma(z){\cdot}\sigma(w)$,
• $\sigma$ est bijective.

Ces propriétés impliquent que $\sigma(0)=\sigma(0+0)=\sigma(0)+\sigma(0)$ et donc $\sigma(0)=0$. Elles impliquent également que $\sigma(1)=\sigma(1{\cdot}1)=\sigma(1){\cdot}\sigma(1)$, d’où on déduit que $\sigma(1)=1$ ou $\sigma(1)=0$, puis finalement que $\sigma(1) = 1$ car il doit être différent de $\sigma(0)$.

L’ensemble des automorphismes de $\mathbb C$ sera noté $\text{Aut}(\mathbb C)$. Si $\sigma_1$ et $\sigma_2$ sont dans $\text{Aut}(\mathbb C)$, il en est de même de leur composée $\sigma_2\circ\sigma_1$, et de leurs inverses : les mathématiciens disent que $\text{Aut}(\mathbb C)$ est un groupe.

Nous ne connaissons explicitement que deux automorphismes de $\mathbb C$ : l’identité $\text{id}_{\mathbb C} : z\mapsto z$, et la conjugaison complexe : $\sigma(a+bi)=a-bi$, écrit comme $z\mapsto\overline{z}$. C’est un bon exercice (que l’on laisse au lecteur) de montrer que ce sont les seuls qui sont continus. Par contraste, si l’on ne se restreint pas aux automorphismes continus, on peut montrer que $\text{Aut}(\mathbb C)$ est très grand (de même cardinal que l’ensemble des sous-ensembles de $\mathbb R$). Par exemple, sachant que $\sqrt{2}$ est irrationnel (voir [Du-Le] pour 65 preuves de ce fait), on peut considérer l’application $a + b \sqrt 2 \mapsto a – b \sqrt 2$ (qui est définie sur l’ensemble $K$ des nombres de la forme $a + b \sqrt 2$ avec $a$ et $b$ dans l’ensemble $\mathbb Q$ des nombres rationnels) et montrer que celle-ci se prolonge en un automorphisme de $\mathbb C$. Cette dernière propriété de prolongement se généralise à tout automorphisme $\sigma : K \to K$ où $K$ est un sous-ensemble de $\mathbb C$ stable par addition, soustraction, multiplication et division (on appelle cela un sous-corps de $\mathbb C$). Ceci permet d’obtenir beaucoup d’automorphismes de $\mathbb C$.

Beaucoup de questions qu’on peut se poser sur les propriétés algébriques de nombres complexes sont ouvertes. Par exemple, on sait que les nombres $e$ et $\pi$ sont transcendants, c’est-à-dire qu’ils ne sont pas racine d’un polynôme $x^n+a_{n-1}x^{n-1}+\cdots+a_0$ à coefficients $a_i$ dans $\mathbb Q$. Cela implique qu’il existe un $\sigma$ dans $\text{Aut}(\mathbb C)$ tel que $\sigma(e)=\pi$, et aussi qu’il existe un $\sigma$ dans $\text{Aut}(\mathbb C)$ tel que $\sigma(\pi)=e$. On s’attend à ce que $e$ et $\pi$ soient algébriquement indépendants (c.à.d., qu’il n’existe pas de polynôme non nul $f$ dans $\mathbb Q[x,y]$ tel que $f(e,\pi)=0$). Toutefois, on ne connait pas, à ce jour, de démonstration de ce fait. On ne sait pas non plus s’il existe un $\sigma$ dans $\text{Aut}(\mathbb C)$ qui échange $e$ et $\pi$.

La symétrie de Galois en théorie des nombres

Abordons la théorie de Galois. Soit $f = x^n+a_{n-1}x^{n-1}+\cdots+a_0$ un polynôme à coefficients $a_i$ dans $\mathbb Q$. Le théorème fondamental d’algèbre nous dit que l’équation $f(z)=0$ a exactement $n$ solutions dans $\mathbb C$, comptées avec multiplicité. Écrivons $\text{Racines}(f)$ pour l’ensemble de ces racines. Pour $\sigma$ dans $\text{Aut}(\mathbb C)$ et $z$ dans $\text{Racines}(f)$ on a

$$\begin{array}{rcl}
0 & = & \sigma(0) = \sigma(f(z))= \sigma(z^n+\cdots+a_1z+a_0) \\
&= &\sigma(z^n)+\cdots+\sigma(a_1z) + \sigma(a_0) \\
&= &\sigma(z)^n +\cdots+\sigma(a_1)\sigma(z)+\sigma(a_0) \\
&= &\sigma(z)^n +\cdots+a_1\sigma(z)+a_0 = f(\sigma(z))
\end{array}$$

et donc $\sigma(z)$ est encore dans $\text{Racines}(f)$. Nous en concluons que chaque $\sigma$ dans $\text{Aut}(\mathbb C)$ permute les éléments de $\text{Racines}(f)$. Le groupe de Galois de $f$ est défini comme l’ensemble $\text{Gal}(f)$ des permutations de $\text{Racines}(f)$ induite s par des éléments de $\text{Aut}(\mathbb C)$.

Regardons quelques exemples. Soit $f$ le polynôme $x^2-4$. Alors $\text{Racines}(f)$ est l’ensemble $\{-2,2\}$. Or, les deux éléments de cet ensemble sont fixés par tous les $\sigma$ de $\text{Aut}(\mathbb C)$ ; en effet, on a déjà vu qu’un $\sigma \in \text{Aut}(\mathbb C)$ envoie nécessairement $1$ sur $1$, il envoie donc aussi $1+1 = 2$ sur $\sigma(1) + \sigma(1) = 1+1 = 2$. Le même raisonnement montre qu’il envoie également $-2$ sur lui-même. Au final, $\text{Gal}(f)$ ne contient que la permutation identité $2\mapsto 2$, $-2\mapsto -2$.

Pour $g=x^2+4$, nous avons $\text{Racines}(g)=\{2i,-2i\}$. Cette fois-ci, il existe un élément de $\text{Aut}(\mathbb C)$ qui échange ces deux racines : c’est la conjugaison complexe. Donc $\text{Gal}(g)$ contient les deux permutations possibles des deux racines : l’identité, et celle qui échange les deux racines : $2i\mapsto -2i$, $-2i\mapsto 2i$.

Pour $h=x²-2$, les racines sont $\sqrt 2$ et $-\sqrt 2$ et nous avons déjà dit qu’il existe un $\sigma$ dans $\text{Aut}(\mathbb C)$ qui permute ces deux nombres. Donc $\text{Gal}(h)$ contient les deux permutations possibles de $\{\sqrt{2},-\sqrt{2}\}$.

Revenons à la théorie générale. Celle-ci a été initialement inventée pour résoudre le problème de la résolution par radicaux des équations algébriques. Cependant, elle connaît maintenant beaucoup d’autres applications, à la fois en théorie et en calcul.

Les lecteurs intéressés par la possibilité de calculer des groupes de Galois sont invités à installer le logiciel gratuit PARI/GP (voir [PARI]) et à se servir de la commande polgalois, qui calcule $\text{Gal}(f)$ pour des polynômes de degré au plus $11$.

Nous nous proposons dans la suite de cet article d’expliquer comment, dans les très grandes lignes, elle intervient dans la démonstration par Wiles et Taylor-Wiles du grand théorème de Fermat.

Représentations galoisiennes de dimension un et deux

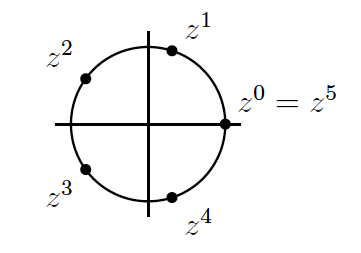Des exemples importants de polynômes sont ceux associés à la division du cercle en $n$ parts égales ou, ce qui revient au même, aux polygones réguliers. Soit $n>1$, $f=x^n-1$, et $z=e^{2i\pi/n} = \cos(\frac{2\pi} n)+i\sin(\frac{2\pi}n)$. L’application

$$\{0,1,\ldots,n{-}1\} \to \text{Racines}(f), \quad a\mapsto z^a$$

est alors bijective ; nous l’appellerons un étiquetage des racines de $f$. L’illustration ci-contre concerne le cas $n=5$.

Les relations algébriques entre les racines de $f$ (qui sont toutes des puissances de $z$) fournissent des contraintes sur les permutations données par les $\sigma$ dans $\text{Aut}(\mathbb C)$. En effet, si $\sigma(z)$ est connu, il en est alors de même de tous les $\sigma(z^a)$ puisque ceux-ci doivent être égaux à $\sigma(z)^a$. Par ailleurs, comme $\sigma(z)$ est une racine de $f$, il prend la forme $z^k$ pour un certain entier $k$ dans $\{0,1,\ldots,n{-}1\}$ uniquement déterminé. De $z^n=1$ et $z^d\neq 1$ pour tout $d$ avec $1\leq d < n$, on déduit que $\text{pgcd}(k,n)=1$. Ainsi les permutations dans $\text{Gal}(f)$ sont de la forme $z^a\mapsto z^{ka}$, avec $0\leq k< n$ et $\text{pgcd}(n,k)=1$. Gauss a montré que toutes les permutations précédentes apparaissent dans $\text{Gal}(f)$.

En termes de l’étiquetage $\{0,1,\ldots,n{-}1\} \to \text{Racines}(f)$, $a\mapsto z^a$, le groupe $\text{Gal}(f)$ est donc exactement formé des permutations de $\{0,1,\ldots,n{-}1\}$ de la forme $a\mapsto ka \text{ mod } n$, avec $0\leq k< n$ et $\text{pgcd}(n,k)=1$. Ici $b \text{ mod } n$ désigne le reste de la division euclidienne de $b$ par $n$. Par exemple, la conjugaison complexe correspond a la multiplication par $k=-1$ (ou plutôt $n{-}1$, mais cela a le même effet sur les restes modulo $n$), car $\overline{z}=\overline{e^{2\pi i/n}}=e^{-2\pi i/n}=z^{-1}$.

Dans cet exemple, la façon dont le groupe de Galois permute les racines (on parle souvent d’action du groupe de Galois) est donc très simple : si l’on numérote convenablement les racines, l’action se résume à une multiplication. Une telle donnée est ce que l’on appelle une représentation galoisienne de dimension 1.

On peut dire que pendant longtemps les mathématiciens ont essayé de démontrer le théorème de Fermat par l’étude de ces représentations galoisiennes (racines de l’unité, corps cyclotomiques), et que finalement c’est en étudiant celles de dimension 2 qu’ils y sont parvenus.

Qu’est-ce qu’une telle représentation ? L’idée de base est qu’au lieu d’étiqueter les racines par les entiers entre $0$ et $n-1$, on les étiquette par des couples de tels entiers, la notion de multiplication dans cette nouvelle situation étant légèrement différente et explicitée dans la définition précise ci-dessous [1].

Définition. Une représentation galoisienne de dimension 2 est un polynôme

$$f=x^{n^2}+\cdots+a_1x+a_0$$

de degré $n^2$, avec les $a_i$ dans $\mathbb Q$, qui est donné avec un étiquetage de $\text{Racines}(f)$ par les couples $v=(v_1, v_2)$ avec $v_1$ et $v_2$ dans $\{0,1,\ldots,n{-}1\}$, le tout étant soumis à la condition suivante : le groupe de Galois $\text{Gal}(f)$ est constitué de permutations de la forme

$$(v_1, v_2) \mapsto ((a v_1 + b v_2) \text{ mod } n, (c v_1 + d v_2)
\text{ mod } n)$$

où $a$, $b$, $c$ et $d$ sont des entiers tels que $ad-bc$ soit premier avec $n$.

Remarque. Pour se rappeler qu’on a fixé un entier $n$ dans cette histoire, les mathématiciens disent en général que la représentation galoisienne est à coefficients dans $\mathbb Z/n\mathbb Z$.

Ces objets jouent un rôle très important dans la preuve par Wiles du théorème de Fermat (voir [Wi, Ta-Wi]). Depuis une quarantaine d’années l’étude de telles représentations occupe une place centrale en arithmétique (c’était le début du « Programme de Langlands »). La différence essentielle avec le cas de dimension 1 est la non-commutativité : lorsque l’on compose deux permutations prenant la forme donnée dans la définition précédente, l’ordre des facteurs est important.

Courbes elliptiques

Nous avons vu que le polynôme $x^n-1$ donne une représentation galoisienne de dimension 1. Nous allons voir que certains polynômes associés aux courbes elliptiques fournissent, eux, des représentations galoisiennes de dimension 2.

Une courbe elliptique (sur l’ensemble $\mathbb Q$ des nombres rationnels) est une courbe dans le plan donnée par une équation de la forme $y^2=x^3+ax+b$ avec $a$ et $b$ dans $\mathbb Q$, tels que le polynôme $x^3+ax+b$ n’ait pas de racine multiple dans $\mathbb C$, c’est-à-dire tel que $4a^3+27b^2$ soit non nul. Dans la figure ci-dessous (trouvée sur Wikipedia) on voit la courbe d’équation $y^2=x^3-x+1$ dans le plan réel ainsi que quelques unes de ses intersections avec des droites.

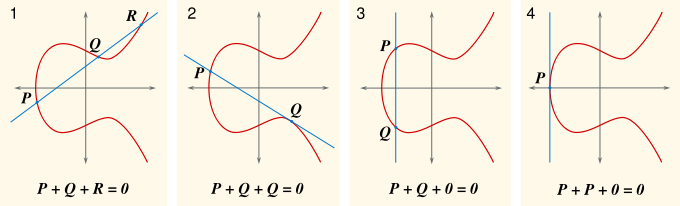Une courbe elliptique et sa loi d’addition

Comme l’équation de la courbe est de degré 3, chaque droite dans le plan a au plus 3 points d’intersection avec la courbe. En fait, si on compte ces points d’intersections avec multiplicité et si on accepte les points dont les coordonnées sont complexes, chaque droite d’équation $y=cx+d$ avec $c$ non nul en a exactement 3, et chaque droite verticale (d’équation $x=c$) en a 2. Pour avoir 3 points d’intersection dans tous les cas, on ajoute traditionnellement sur la courbe elliptique un « point à l’infini » noté $0$ (zéro) — on justifiera plus loin cette notation en convenant que celui-ci est sur toutes les droites verticales. Nous notons $E$ la courbe complexe complétée, c’est-à-dire l’ensemble $\{(x,y)\in\mathbb C^2 :y^2=x^3+ax+b\}\cup\{0\}$.

Si maintenant on a deux points $P$ et $Q$ sur la courbe $E$, on prend la droite qui passe par $P$ et $Q$ (la droite tangente si $P=Q$, et oublions le cas où $P=Q=0$). Cela nous donne un troisième point d’intersection, disons $R$. Le symétrique de $R$ par rapport à l’axe des abscisses est alors noté $P+Q$. On peut démontrer que pour tous $P$, $Q$ et $R$ dans $E$, on a $P+0 = P$ (c’est immédiat), $(P+Q)+R=P+(Q+R)$ (c’est difficile), $P+Q=Q+P$ (c’est immédiat), et que pour tout $P$ il existe un $Q$ tel que $P+Q=0$ (prendre pour $Q$ le symétrique de $P$ par rapport à l’axe des abscisses). Ceci justifie la notation $P+Q$ ainsi que la notation $0$ pour le point à l’infini.

Un autre fait classique et à nouveau difficile dit que pour chaque entier $n\geq1$, l’ensemble $E[n]$ des points $P$ de $E$ tel que la somme $P+\cdots+P$ avec $n$ termes vaut $0$ est formé de $n^2$ éléments. Mieux encore : il existe une bijection (étiquetage) entre cet ensemble $E[n]$ et l’ensemble des couples $(v_1, v_2)$ avec $v_1$ et $v_2$ dans $\{0, \ldots, n{-}1\}$, et cette bijection est compatible avec les lois d’additions des deux côtés, dans le sens où si $P$ correspond à $(v_1, v_2)$ et $Q$ à $(w_1,w_2)$, alors $P+Q$ correspond à $((v_1+w_1) \text{ mod } n, (v_2+w_2) \text{ mod } n)$. La démonstration est difficile : elle demande de réinterpréter de $E$ à l’aide de fonctions complexes méromorphes de Weierstrass ; n’en disons pas davantage…

D’autre part, comme la courbe $E$ est définie par une équation à coefficients dans $\mathbb Q$, la loi d’addition sur $E$ est compatible avec tout $\sigma$ dans $\text{Aut}(\mathbb C)$ : pour tous $P$ et $Q$ dans $E$ on a $\sigma(P+Q)=\sigma(P)+\sigma(Q)$ où on a posé, pour $P=(x,y)$ avec $x$ et $y$ dans $\mathbb C$, $\sigma(P)=(\sigma(x),\sigma(y))$. Il en résulte que pour $\sigma$ dans $\text{Aut}(\mathbb C)$ et $P$ dans $E[n]$, on a $\sigma(P)$ dans $E[n]$. De cela, on peut déduire que les points de $E[n]$ se décrivent à l’aide des racines d’un polynôme $f$ de degré $n^2$. Pour obtenir cette description, on choisit un point convenable $C$ dans $\mathbb Q^2$, et on associe à $P$ dans $E[n]$ l’abscisse du point d’intersection de la droite passant par $C$ et $P$ avec l’axe des abscisses. La propriété de compatibilité à l’action de $\text{Aut}(\mathbb C)$ implique alors que les $n^2$ abscisses correspondant aux $n^2$ points de $E[n]$ apparaissent comme les racines d’un polynôme à coefficients rationnels [2].

Si l’on revient à la définition et que l’on met ensemble tout ce qui a été dit précédemment, on se rend compte que le polynôme que l’on vient de construire définit une représentation galoisienne de dimension 2.

Terminons par un tout petit exemple. Soit $E$ la courbe complétée donnée par $y^2=x^3-x+1$. Prenons $n=2$. Alors $E[2]$ est l’ensemble des quatre points $0$, $(z_1,0)$, $(z_2,0)$ et $(z_3,0)$ où $z_1$, $z_2$ et $z_3$ sont les racines de $x^3-x+1$. Si l’on choisit comme point $C$ celui de coordonnées $(0,1)$, les abscisses correspondant aux quatre points précédents sont $0$, $z_1$, $z_2$ et $z_3$ et le polynôme dont ce sont les racines est $f = x(x^3-x+1)$. Le groupe de Galois de ce polynôme est formé de toutes les permutations de l’ensemble $\text{Racines}(f) = \{0, z_1, z_2, z_3\}$ qui laissent fixe $0$ : il est clair que si une permutation des racines de $f$ provient d’un automorphisme de $\mathbb C$, alors elle laisse fixe $0$ et, pour montrer l’égalité, on peut utiliser PARI/GP pour s’assurer que le groupe de Galois de $x^3-x+1$ contient toutes les permutations de $\{z_1, z_2,z_3\}$. Enfin, si l’on étiquette les racines comme suit

$$0 \leftrightarrow (0,0) \quad ; \quad
z_1 \leftrightarrow (1,0) \quad ; \quad
z_2 \leftrightarrow (0,1) \quad ; \quad
z_3 \leftrightarrow (1,1)$$

on peut vérifier, en regardant séparément tous les cas par exemple, que les 6 éléments de $\text{Gal}(f)$ peuvent se mettre sous la forme imposée dans la définition d’une représentation galoisienne de dimension 2 ; par exemple la permutation qui envoie $z_1$ sur $z_2$, $z_2$ sur $z_3$ et $z_3$ sur $z_1$ s’écrit $(v_1, v_2) \mapsto (v_2, (v_1+v_2) \text{ mod } 2)$.

Le grand théorème de Fermat

Le grand théorème de Fermat est un énoncé qui affirme que, dès que $n$ est un entier supérieur ou égal à 3, l’équation $x^n + y^n = z^n$ n’a pas de solutions en nombres entiers strictement positifs. Il apparaît pour la première fois au 17ème siècle dans un manuscrit de Pierre de Fermat, sans démonstration. Depuis, de nombreuses générations de mathématiciens ont tenté de démontrer ce résultat avec, au fil des siècles, de nombreux progrès significatifs (qui ont conduit notamment au développement de la théorie algébrique des nombres). La première démonstration complète a été donnée par Wiles et Taylor-Wiles en 1995. Elle fait intervenir de façon centrale les représentations galoisiennes de dimension 2, et notamment celles liées aux courbes elliptiques.

La découverte d’un lien entre théorème de Fermat et courbes elliptiques semble dater de 1969. Elle apparaît dans un exposé par Hellegouarch à Bordeaux (voir [He2], et l’appendice de [He1]). La question que se posait Hellegouarch était de savoir si une courbe elliptique $E$ (sur $\mathbb Q$) pouvait avoir un point $P=(x,y)$ dans $E[n]$ avec $x$ et $y$ dans $\mathbb Q$ et $n$ « grand ». Sous certaines hypothèses, il montrait que si cela se produisait, alors le théorème de Fermat serait faux en degré $n$.

En 1985, Frey a étudié la question dans l’autre sens : peut-on démontrer le théorème de Fermat en montrant que la courbe elliptique associée par Hellegouarch à un contre-exemple ne peut exister ? Pour appuyer son idée, il a également remarqué que l’existence d’une telle courbe elliptique contredirait la conjecture dite de modularité (on en dira quelques mots dans la suite), très importante en mathématiques.

Après ceci, les choses sont allées vite. Dans un article en 1987, Serre a précisé et généralisé les idées de Frey en les plaçant dans le contexte des représentations galoisiennes, et en formulant une conjecture précise. Ensuite, Ribet a montré une partie suffisante de la conjecture de Serre pour en déduire que la conjecture de modularité implique le théorème de Fermat. Finalement, Wiles et Taylor-Wiles ont démontré à nouveau une partie suffisante de la conjecture de modularité pour en déduire le théorème de Fermat. Nous n’allons pas détailler davantage toute cette histoire (voir la dernière partie En lire plus), notre but étant plutôt ici d’indiquer le rôle joué par les représentations galoisiennes. C’est ce que nous allons essayer de faire tout de suite.

Le rôle des représentations galoisiennes

Pour démontrer le théorème de Fermat, il suffit de supposer qu’il existe une solution à l’équation de Fermat $x^n + y^n = z^n$ et d’en déduire une contradiction. Comme on sait déjà (depuis les travaux de Fermat lui-même et de Gauss) que le théorème est vrai en degré 3 et 4, on peut supposer que l’exposant $n$ est un nombre premier $p\geq5$. Soit donc $p\geq5$ premier, et $a$, $b$ et $c$ dans $\mathbb Z$ tels que $a^p+b^p+c^p=0$, avec $abc\neq0$. On peut supposer que $a$, $b$ et $c$ sont premiers entre eux deux par deux et, quitte à les permuter, que $b$ est pair et $a+1$ est divisible par $4$. Posons $A=a^p$, $B=b^p$, et $C=c^p$ et, en suivant Hellegouarch et Frey, considérons la courbe elliptique $E_{A,B,C}$ sur $\mathbb Q$ donnée par :

$$E_{A,B,C}\,\colon\quad y^2 = x(x-A)(x+B).$$

Il se trouve que cette courbe $E_{A,B,C}$ possède des propriétés qui rendent son existence impossible. La première d’entre elles est la non-ramification en dehors de 2 et $p$ de la représentation galoisienne $E_{A,B,C}[p]$. Cela signifie que pour tout nombre premier $\ell$ différent de 2 et de $p$, dans des coordonnées convenables, les points $P$ de $E_{A,B,C}[p]$ restent distincts après réduction modulo $\ell$ (si ces points sont à coordonnées entières, cela signifie simplement « après avoir pris leur reste dans la division euclidienne par $\ell$ », sinon la notion est plus compliquée). La démonstration de cette propriété utilise des outils « standard » : il s’agit du calcul du discriminant du polynôme $x(x-A)(x+B)$ (qui apparaît dans la définition de la courbe elliptique), qui vaut $A^2B^2(A+B)^2=(ABC)^2=(abc)^{2p}$ et a donc la propriété remarquable d’être une puissance $p$-ième. En utilisant un argument analogue, on démontre aussi une propriété un peu plus faible pour la réduction en $\ell = p$.

La seconde propriété que l’on utilise est la modularité des courbes elliptiques qui découle de la (partie de la) conjecture de modularité démontrée par Wiles et Taylor-Wiles. Il serait trop long d’expliquer exactement ici la conjecture de modularité ; pour le propos de cet article, ce qu’il est important de retenir est qu’elle prédit en particulier que la représentation galoisienne $E_{A,B,C}[p]$ peut s’obtenir par un autre moyen complètement différent faisant intervenir ce que l’on appelle des formes modulaires (qui sont des objets de nature analytique n’ayant a priori pas de rapport avec les courbes elliptiques). Le lecteur désireux d’en savoir davantage pourra se reporter à [Di-Sh].

Enfin, en étudiant les formes modulaires, on peut démontrer qu’une représentation galoisienne construite à partir d’une forme modulaire ne saurait vérifier la propriété de non-ramification que l’on a évoquée précédemment. C’est là qu’apparaît la contradiction, de laquelle découle le théorème de Fermat.

En réalité, la conjecture de modularité, qui lie les courbes elliptiques aux formes modulaires, peut s’énoncer sans représentations galoisiennes. Toutefois, d’une part, comme nous venons de l’expliquer, c’est bien à travers les représentations galoisiennes que la contradiction (de laquelle découle le théorème de Fermat) apparaît et, d’autre, part, la preuve de Wiles et Taylor-Wiles ne pourrait se faire sans les représentations galoisiennes. Par exemple, dans cette preuve, on passe d’abord de la courbe elliptique $E$ au système des représentations galoisiennes $(E[3^n])_{n\geq1}$. Si nous étions physiciens, nous dirions que ce sont les représentations galoisiennes qui portent les forces entre le théorème de Fermat, les courbes elliptiques et les formes modulaires.

Pour finir, signalons que depuis les résultats plus récents de Khare-Wintenberger et Kisin, qui démontrent la conjecture de Serre évoquée plus haut, il y a une preuve un peu plus directe du théorème de Fermat, mais qui passe elle encore plus par les représentations galoisiennes.

En lire plus

De bonnes références pour lire plus sur ce sujet (l’histoire de la preuve du théorème de Fermat, théorie des formes modulaires et modularité des courbes elliptiques sur $\mathbb Q$) sont les livres d’Hellegouarch [He1, He2] et le livre de Diamond et Shurman [Di-Sh], ainsi que les exposés au Séminaire Bourbaki [Se] et [Oe].

Bibliographie

[Di-Sh] F. Diamond and J. Shurman, A first course in modular forms GTM 228, Springer, Berlin, 2005

[Du-Le] Ludmila Duchêne et Agnès Leblanc, Rationnel mon $\mathbb Q$, Hermann éditeurs, 2010

[He1] Yves Hellegouarch, Invitation aux mathématiques de Fermat-Wiles, Enseignement des Mathématiques. Masson, Paris, 1997. ISBN : 2-225-83008-8

[He2] Yves Hellegouarch, Points d’ordre fini des variétés abéliennes de dimension un., Colloque de Théorie des Nombres (Univ. Bordeaux, Bordeaux, 1969). Bull. Soc. Math. France, Mem. 25, Soc. Math. France, Paris, 1971

[Oe] J. Oesterlé, Travaux de Wiles (et Taylor…). II., Séminaire Bourbaki, Vol. 1994/95, Astérisque No. 237 (1996), Exp. No. 804, 5, 333–355

[PARI] C. Batut, K. Belabas, D. Bernardi, H. Cohen, and M. Olivier, a href=”http://pari.math.u-bordeaux.fr”>User’s guide to PARI/GP (version 2.3.1)

[Se] J-P. Serre, Travaux de Wiles (et Taylor…). I., Séminaire Bourbaki, Vol. 1994/95, Astérisque No. 237 (1996), Exp. No. 803, 5, 319–332

[Ta-Wi] R. Taylor and A. Wiles, Ring-theoretic properties of certain Hecke algebras, Ann. of Math. (2) 141 (1995), no. 3, 553–572

[Wi] A. Wiles, Modular elliptic curves and Fermat’s last theorem, Ann. of Math. (2) 141 (1995), no. 3, 443–551

Notes

[1] Ceux qui connaissent les matrices reconnaitront la multiplication d’une matrice $2 \times 2$ par un vecteur.

[2] Pour construire le polynôme, on peut simplement prendre le produit des $(x-x_i)$ où les $x_i$ sont ces abscisses. La difficulté est alors de montrer que le polynôme obtenu est à coefficients rationnels, et c’est à ce moment que l’on utilise la compatibilité à l’action de $\text{Aut}(\mathbb C)$.