par X. Caruso
Alors qu’il étudiait la théorie des équations algébriques, Évariste Galois (1811-1832) s’est rendu compte que l’on pouvait l’appliquer non seulement aux équations algébriques usuelles du type
$$x^5 – 10 x^3 + 5 x^2 + 10 x + 1 = 0$$
mais aussi aux « congruences », c’est-à-dire aux équations prenant la forme
$$7 \quad \text{divise} \quad x^5 – 10 x^3 + 5 x^2 + 10 x + 1.$$
De même qu’on est parfois obligé d’introduire des nombres complexes pour résoudre les équations du premier type, Galois invente de nouveaux nombres imaginaires — les imaginaires de l’arithmétique — servant à résoudre celles du second type.
En réalité, Galois n’est pas le premier à avoir découvert ses nouveaux nombres : Carl Friedrich Gauss (1777-1855) était déjà arrivé aux mêmes conclusions quelques années avant lui. Toutefois, le texte de Gauss étant resté non publié, Galois n’en a jamais eu connaissance.
Dans cet article, on présente la construction et l’étude qu’a faite Galois des imaginaires de l’arithmétique, en collant le plus possible à ses idées initiales telles qu’elles sont présentées dans son article Sur la théorie des nombres publié au bulletin des sciences mathématiques, physiques et chimiques en 1830.
Les congruences : qu’est que c’est ?
Avant d’entrer dans le vif du sujet, expliquons plus en détails ce qu’est une congruence et quelles sont les similarités entre les équations algébriques usuelles et celles sur les congruences. La notion de congruence est relativement simple et, en tout cas, bien antérieure à Galois : par exemple, le mathématicien suisse Leonhard Euler (1707-1783) avait déjà parfaitement compris son intérêt et la manipulait avec une aisance redoutable.
Pour la comprendre, on peut commencer à répartir les nombres entiers en un certain nombre de colonnes, disons $7$ pour fixer les idées, comme ci-dessous :
$$\begin{array}{|c|c|c|c|c|c|c|}
\hline
0 & 1 & 2 & 3 & 4 & 5 & 6 \\
7 & 8 & 9 & 10 & 11 & 12 & 13 \\
14 & 15 & 16 & 17 & 18 & 19 & 20 \\
21 & 22 & 23 & 24 & 25 & 26 & 27 \\
28 & 29 & 30 & \cdots & & & \\
\hline
\end{array}$$
La première colonne contient alors les multiples de $7$, la seconde les successeurs de ces nombres, et ainsi de suite. Plutôt qu’aux nombres eux-mêmes, nous allons nous intéresser aux colonnes. Que peut-on faire avec celles-ci ? Eh bien, tout d’abord, on peut les additionner. Par exemple, pour additionner la colonne de 2 (c’est-à-dire la troisième colonne, donc, suivez bien) et la colonne de 6 (la dernière), on choisit un nombre dans chacune de ces deux colonnes, on les additionne et on regarde dans quelle colonne le résultat tombe. Si on choisit, disons, $9$ et $20$, on a à calculer $9 + 20$, cela fait $29$, et on voit dans le tableau que ce dernier nombre est dans la colonne de $1$ ; ainsi on a
$$(\text{Colonne de } 2) + (\text{Colonne de } 6) = (\text{Colonne de } 1).$$
Si on avait choisi d’autres nombres (on dit souvent {représentants}) que $9$ et $20$, l’addition à effectuer n’aurait pas été la même mais le résultat final, lui, n’aurait pas été modifié: on aurait encore trouvé $(\text{Colonne de } 1)$. Bien sûr, au lieu de $9$ et $20$, il aurait été plus intelligent de choisir directement $2$ et $6$ : on n’aurait pas eu à s’embêter à descendre dans les colonnes et l’addition n’aurait pas été plus difficile.
De la même façon, on peut multiplier les colonnes. Pour multiplier la colonne de 2 par celle de 6, on calcule $2 \times 6$ et on trouve $12$ qui est dans la colonne de 5. Ainsi, on écrira
$$(\text{Colonne de } 2) \times (\text{Colonne de } 6) = (\text{Colonne de } 5).$$
On peut également soustraire les colonnes et même les diviser pour peu que le diviseur ne soit pas la colonne de $0$. Toutefois, pour cela, il faut prendre garde de choisir judicieusement les représentants pour que l’opération effectuée ait pour résultat un entier écrit dans le tableau. Typiquement, si l’on veut soustraire la colonne de 6 à celle de 2, on ne peut pas faire l’opération $2-6$ car son résultat est un nombre négatif qui n’apparaît pas dans le tableau. Par contre, si au lieu de $2$, on choisit $9$, l’opération devient $9-6$ et a pour résultat l’entier positif $3$ ; il suit de cela que
$$(\text{Colonne de } 2) – (\text{Colonne de } 6) = (\text{Colonne de } 3).$$
Cela fonctionne de la même manière pour la division, sauf qu’il est plus délicat dans ce cas de trouver une opération qui tombe juste. Malgré tout, on y arrive en général sans grande difficulté : en gardant les mêmes colonnes que précédemment, on peut par exemple choisir $30$ dans la colonne de $2$ et $6$ dans la colonne de $6$. La division $30 \div 6$ tombe alors juste et a pour résultat $5$. D’où :
$$(\text{Colonne de } 2) \div (\text{Colonne de } 6) = (\text{Colonne de } 5).$$
Attention, malgré tout, certaines divisions ne sont pas possibles ! Ce sont celles pour lesquelles on divise par la colonne de $0$. Pour illustrer cela, supposons que l’on souhaite calculer $(\text{Colonne de } 2) \div (\text{Colonne de } 0)$. Pour y parvenir, il nous faudrait pouvoir choisir un élément de la colonne de $2$ qui soit multiple d’un autre élément de la colonne de $0$. Mais manifestement cela n’est pas possible puisque aucun nombre de la colonne de $2$ n’est multiple de $7$ alors que tous les nombres de la colonne de $0$ le sont; ainsi, dans la fraction $\frac{\text{représentant de } 2}{\text{représentant de } 0}$, il y aura toujours un facteur $7$ au dénominateur qui ne pourra être éliminé, et le quotient ne pourra jamais être entier.
Par contre, hormis ce cas (celui de la division par la colonne de $0$), toutes les divisions sont possibles. Si on est courageux, on peut le vérifier en posant toutes les divisions une par une: il n’y en a jamais que $42$ ($7$ choix pour le dividende et $6$ pour le diviseur). Si on est fainéant mais savant, on peut utiliser le théorème de Bézout pour arriver au même résultat. L’avantage de la seconde méthode est qu’elle se généralise à un nombre de colonnes qui est un nombre premier quelconque.
La démonstration générale à l’aide du théorème de Bézout
On suppose ici que le nombre de colonnes est un nombre premier, que l’on note $p$. Admettons que l’on veuille diviser la colonne de $a$ par celle de $b$; ici $a$ et $b$ sont des entiers et $b$ n’est pas un multiple de $p$. Pour la colonne de $b$, choisissons simplement le représentant $b$. On est ainsi amené à démontrer qu’il existe dans un colonne de $a$ un multiple de $b$. Or, dans la colonne de $a$, on trouve les nombres de la forme $a+np$ où $n$ est un entier positif. Il nous faut donc montrer qu’il existe $n$ tel que $a+np$ soit multiple de $b$, c’est-à-dire soit égal à $mb$ pour un certain entier $m$. Or, comme $p$ est premier et ne divise pas $b$, ces deux nombres sont premiers entre eux; d’après le théorème de Bézout, il existe des entiers $u$ et $v$ (et on peut choisir $v$ positif) tels que $1 = ub-vp$. En multipliant par $a$, on obtient $a = aub-avp$, soit encore $a + avp = aub$. Il suffit donc de prendre $n= av$ et $m = au$.
Les mathématiciens notent en général $\mathbb F_7$ (ou encore $\mathbb Z/7\mathbb Z$) l’ensemble des sept colonnes précédentes. La lettre $\mathbb F$ signifie {field} — que l’on traduit, en français, dans ce contexte par corps [1] — et rend compte du fait que l’on sait additionner, soustraire, multiplier et diviser (par une quantité non nulle) les éléments de $\mathbb F_7$.
À partir de maintenant, si $x$ est un nombre entier, on notera $\text{Col}(x)$ la colonne où il apparaît. On a ainsi $\text{Col}(x) \in \mathbb F_7$.
Les congruences : à quoi ça sert ?
Regrouper les nombres par colonnes comme on l’a expliqué ci-dessus peut s’avérer d’une grande utilité pour la résolution des équations diophantiennes. L’adjectif “diophantien” vient du mathématicien grec Diophante qui a vécu à Alexandrie au 2ème siècle de notre ère. Il signifie que l’on ne cherche que les solutions entières de l’équation proposée. Par exemple, résoudre l’équation diophantienne
$$x^7 – x = y^2 +1$$
c’est trouver tous les entiers $x$ et $y$ vérifiant cette égalité. Résoudre une telle équation n’est {a priori} pas facile car il y a une infinité de possibilités pour chacune des inconnues $x$ et $y$; il est donc complètement exclu de les tester toutes.
À l’inverse, si $X$ et $Y$ ne désignent maintenant pas des entiers mais des colonnes (ou, autrement dit, des éléments de $\mathbb F_7$), il est possible de procéder à une recherche exhaustive (cela ne fait que $7 \times 7 = 49$ cas à tester: $7$ valeurs possibles pour $X$ et $7$ pour $Y$). Or, si $x$ et $y$ sont des entiers solutions de l’équation, et si on note respectivement $X$ et $Y$ les colonnes dans lesquelles $x$ et $y$ apparaissent, on doit avoir
$$X^7 – X = Y^2 + \text{Col}(1)$$
où, bien entendu, $Y^2$ désigne le produit (de colonnes) $Y \times Y$ et de même pour $X^7$.
Essayons maintenant de résoudre l’équation sur les colonnes. Comme nous le disions précédemment, il suffit pour cela d’énumérer toutes les possibilités pour $X$ et $Y$. Commençons par $Y$. On écrit :
- si $Y = \text{Col}(0)$ (c’est-à-dire si $y$ et $0$ sont dans la même colonne), alors $Y^2+\text{Col}(1) = \text{Col}(1)$;
- si $Y = \text{Col}(1)$, alors $Y^2+\text{Col}(1) = \text{Col}(2)$;
- si $Y = \text{Col}(2)$, alors $Y^2+\text{Col}(1) = \text{Col}(5)$;
- si $Y = \text{Col}(3)$, alors $Y^2+\text{Col}(1) = \text{Col}(3)$;
- si $Y = \text{Col}(4)$, alors $Y^2+\text{Col}(1) = \text{Col}(3)$;
- si $Y = \text{Col}(5)$, alors $Y^2+\text{Col}(1) = \text{Col}(5)$;
- si $Y = \text{Col}(6)$, alors $Y^2+\text{Col}(1) = \text{Col}(2)$;
On remarque, en particulier, que $Y^2+\text{Col}(1)$ ne peut valoir n’importe quoi: il ne peut jamais être égal ni à la colonne de $0$, ni à celle de $4$, ni à celle de $6$.
Passons maintenant à $X$. Après un calcul (qui n’est pas immédiat et qu’on encourage le lecteur à faire), on trouve que quelle que soit la colonne où se trouve $x$, on a toujours $X^7 – X = \text{Col}(0)$. Ce résultat est connu sous le nom de petit théorème de Fermat [2] ; on y reviendra plus loin dans cet article. Pour l’instant, rappelons que $Y^2+\text{Col}(1)$ ne pouvait jamais être la colonne de $0$. Comme $X^7 – X$ est, lui, toujours cette colonne, l’égalité $X^7 – X =Y^2+\text{Col}(1)$ ne peut jamais être vérifiée. L’équation sur les colonnes n’a donc pas de solutions !
Or, on avait dit qu’à partir d’une solution à l’équation diophantienne de départ, on pouvait fabriquer une solution à l’équation sur les colonnes. Comme une telle solution n’existe pas, c’est nécessairement que l’équation diophantienne elle-même n’admet pas de solution. On a donc résolu notre problème.
Une remarque, à ce niveau, s’impose. On a eu beaucoup de chance avec l’exemple précédent (enfin, plutôt, je l’ai choisi pour qu’on en ait) car l’absence de solutions à l’équation sur les colonnes permettait directement de conclure. En général, l’équation sur les colonnes aura des solutions, et il restera encore beaucoup de travail (souvent difficile) pour résoudre complètement l’équation diophantienne. Cela dit, en passant aux colonnes, on obtient souvent des premières informations intéressantes.
Un nombre imaginaire pour résoudre les équations
On vient de voir que l’équation $X^7-X = Y^2 + \text{Col}(1)$ n’a aucune solution dans $\mathbb F_7$ (c’est-à-dire lorsque $X$ et $Y$ sont des colonnes). En fait, comme $X^7-X$ est toujours égal à la colonne de $0$, l’équation
$$Y^2 = -\text{Col}(1)$$
n’a, elle non plus, aucune solution. Autrement dit, on n’a pas de racine carrée de $-1$ dans $\mathbb F_7$ [3]. Sur ce point précis, les « nombres colonne » ressemblent aux nombres réels. Poursuivant l’analogie, on est tenté, comme on le fait lorsque l’on construit les nombres complexes, d’inventer un nouveau nombre $i$ dont le carré serait $-\text{Col}(1)$. C’est exactement ce qu’a proposé Galois dans son article de 1830.
De même que pour les nombres complexes usuels, ce nouveau nombre $i$ ne vient pas tout seul mais avec plein de camarades qui sont les $A+iB$ où, faisons bien attention, $A$ et $B$ sont ici des éléments de $\mathbb F_7$, c’est-à-dire des colonnes. En tout, cela fait $7^2 = 49$ nombres : $7$ possibilités pour la “partie réelle” $A$ et $7$ possibilités pour la “partie imaginaire” $B$. Les opérations usuelles (addition, multiplication, soustraction, division) s’étendent à ces nombres de la même façon qu’elles s’étendent aux nombres complexes : la somme $(A+iB)+(A’+iB’)$ et la différence $(A+iB)-(A’+iB’)$ se calculent simplement en ôtant les parenthèses et en regroupant les parties réelles et imaginaires, le produit $(A+iB)(A’+iB’)$ se calcule en développant et le quotient $\frac{A+iB}{A’+iB’}$ se calcule avec la méthode de la quantité conjuguée :
$$\frac{A+iB}{A’+iB’} = \frac{(A+iB)(A’-iB’)}{(A’+iB’)(A’-iB’)} = \frac{AA’+BB’}{{A’}^2+{B’}^2} + i \: \frac{A’B-AB’}{{A’}^2+{B’}^2}.$$
Bien entendu, ici, le fait que le dénominateur ne s’annule pas dès que $A’$ ou $B’$ n’est pas nul ne s’obtient pas par un argument de positivité (il ne fait aucun sens de dire qu’une colonne est positive ou pas) mais plutôt car, de ${A’}^2+{B’}^2 = 0$, on déduirait que $(\frac{A’}{B’})^2 = -\text{Col}(1)$ et donc qu’il existerait une racine carrée de $-1$ dans $\mathbb F_7$.
L’ensemble des nombres de la forme $A+iB$ est noté $\mathbb F_{49}$ : encore une fois la lettre $\mathbb F$ rend compte du fait que l’on sait faire les opérations usuelles avec ces nombres et l’indice $49$ signifie qu’il y en a $49$. Attention : $\mathbb F_{49}$ n’est en particulier pas du tout l’ensemble des colonnes que l’on obtiendrait en répartissant les nombres entiers dans un tableau à 49 colonnes.
Une propriété remarquable de $\mathbb F_{49}$
Lorsque l’on a résolu l’équation $X^7 – X = Y^2+1$ dans $\mathbb F_7$, on a remarqué que la quantité $X^7 – X$ était toujours nulle quelle que soit la valeur de $X$. Cette propriété étonnante admet un analogue dans $\mathbb F_{49}$ qui est le suivant.
Théorème 1. Tout élément $X = A+iB$ de $\mathbb F_{49}$ vérifie $X^{49} = X$.
Démontrons ce théorème. Pour cela, considérons un élément $X$ de $\mathbb F_{49}$. S’il est nul (c’est-à-dire égal à $\text{Col}(0)$), alors $X^{49}$ est aussi nul, et l’égalité est évidente. Supposons donc maintenant que $X$ ne soit pas nul et regardons le tableau ci-dessous :
$$\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
\text{Col}(1)&
\text{Col}(2)&
\cdots&
i &
i + \text{Col}(1)&
\cdots \\
\hline
X&
X\cdot\text{Col}(2)&
\cdots&
X\cdot i &
X \cdot (i + \text{Col}(1))&
\cdots \\
\hline
\end{array}$$
Dans la première ligne de ce tableau sont écrits, un à côté de l’autre, les $48$ éléments non nuls de $\mathbb F_{49}$. Les nombres de la ligne du dessous, quant à eux, sont obtenus en multipliant par $X$ leur voisin du dessus. Le produit de tous les nombres de la première ligne a pour résultat un nombre non nul que l’on note $P$. Le produit des nombres de la deuxième ligne vaut alors $X^{48} \cdot P$.
Or, on remarque que, dans la seconde ligne, tous les éléments non nuls de $\mathbb F_{49}$ apparaissent une et une unique fois : en effet, un nombre $Y$ apparaît en dessous de $\frac Y X$ et nulle part ailleurs. Du coup, le produit des éléments de la deuxième ligne vaut aussi $P$ puisque l’ordre des facteurs n’a pas d’importance lorsque l’on effectue une multiplication. On en déduit que $X^{48} \cdot P = P$ et donc, en simplifiant par $P$ qui est non nul puis en remultipliant par $X$, que $X^{49} = X$ comme voulu.
En réalité, dans la démonstration que l’on vient de donner, on n’a pas utilisé beaucoup de propriétés de $\mathbb F_{49}$ : si l’on y réfléchit bien, on a simplement utilisé qu’il avait $49$ éléments et que l’on pouvait multiplier et diviser ceux-ci (pourvu que le diviseur ne soit pas zéro). Le même raisonnement montrerait de même que tout $X \in \mathbb F_7$ vérifie $X^7 = X$ (ce que l’on avait déjà vérifié par le calcul plus haut). Il démontre également que si, par la suite, on construit un $\mathbb F_q$ possédant $q$ éléments que l’on peut multiplier et diviser (ce qui ne manquera pas d’arriver), alors tout élément $X$ de ce $\mathbb F_q$ vérifiera $X^q = X$.
Des nouveaux nombres à n’en plus finir
Les nombres complexes usuels jouissent d’une propriété agréable: toute équation algébrique (c’est-à-dire de la forme $a_n x^n + \cdots + a_1 x + a_0 = 0$) admet une solution. Autrement dit, certes l’équation $x^2 = -1$ n’admet pas de solution parmi les nombres réels mais, une fois que l’on ajoute cette solution, on n’a plus de nouveau problème d’équation insoluble.
On peut se poser la même question ici. On a ajouté à $\mathbb F_7$ une solution de l’équation $Y^2 = -\text{Col}(1)$ pour obtenir un nouvel ensemble de nombres que l’on a appelé $\mathbb F_{49}$. Est-il vrai, maintenant, que toutes les équations sont solubles dans $\mathbb F_{49}$ ? Le théorème qu’on a démontré dans la partie précédente permet de répondre à cette question. En effet, puisque l’on sait que $X^{49} = X$ pour tout $X \in \mathbb F_{49}$, l’équation algébrique $X^{49} = X+1$ n’a manifestement pas de solution dans cet ensemble de nombres ! En réalité, on n’est pas obligé de monter à des degrés aussi élevés pour trouver des équations insolubles: on peut déjà en trouver en degré $2$ à condition de prendre des coefficients dans $\mathbb F_{49}$ [4], et même, plus généralement, en tout degré supérieur ou égal à $2$. Par exemple, en degré $3$, l’équation $X^3 = \text{Col}(2)$ n’a pas de solution dans $\mathbb F_{49}$ [5].
De même que tout à l’heure, on ne reste pas bloqué sur ce constat et on progresse en inventant encore un nouveau nombre, disons $j$ cette fois-ci, solution de l’équation, c’est-à-dire vérifiant $j^3 = \text{Col}(2)$. Cette fois-ci, les nombres de la forme $A+jB$ ne sont pas stables par multiplication car le produit de telles quantités va faire intervenir des $j^2$ qui ne vont pas se simplifier ; en effet, on peut bien remplacer $j^3$ par $\text{Col}(2)$, mais on ne sait rien sur $j^2$. On s’en sort, malgré tout, en considérant un espace de nombres encore un peu plus grand, ceux de la forme
$$A + Bj + Cj^2 \quad \text{avec } A, B, C \in \mathbb F_{49}.$$
Ceux-ci sont stables par addition, soustraction, et aussi par multiplication: pour calculer un produit, on développe, et dans le résultat obtenu, on remplace les $j^3$ par $\text{Col}(2)$ et les $j^4$ par $\text{Col}(2) j$.
Ils sont également stables par division, ce qui est, cette fois-ci, nettement plus difficile à démontrer, la méthode de la quantité conjuguée ne fonctionnant plus aussi facilement. Voici néanmoins la formule que l’on trouve :
$$\begin{array}{l}
\frac {A+Bj+Cj^2} {A’+B’j+C’j^2} \\
\hspace{1.5cm} = \frac{A{A’}^2 + 2B{B’}^2 + 4C{C’}^2 – 2AB’C’ -2A’BC’ – 2A’B'C}{{A’}^3+2{B’}^3+4{C’}^3-6A’B'C’} \\
\hspace{1.7cm} + \frac{2A{C’}^2 + {A’}^2B + 4{B’}^2C -AA’B – 2BB’C – 4A’CC’}{{A’}^3+2{B’}^3+4{C’}^3-6A’B'C’} \: j \\
\hspace{1.7cm} + \frac{A{B’}^2 + 2B{C’}^2 + {A’}^2C -AA’C – A’BB’ – 2B’CC’}{{A’}^3+2{B’}^3+4{C’}^3-6A’B'C’}\: j^2
\end{array}$$
Comme vous le constatez vous-même, cette formule n’est pas très ragoûtante. Elle ne sera en fait jamais utilisée dans la suite. Inutile donc de s’acharner à la comprendre dans les moindres détails; le plus important à remarquer est que le résultat de la division (c’est-à-dire le membre de droite) est encore de la forme $(\cdots) + (\cdots)j + (\cdots)j^2$. Autrement dit, en divisant, on n’obtient pas encore de nouveaux nombres qui n’avaient pas été introduits jusqu’à présent.
Après avoir adjoint la quantité $j$, nous sommes maintenant en présence de $49^3 = 117649$ nombres : il y a $49$ possibilités pour le $A$, $49$ pour le $B$ et encore $49$ pour le $C$. L’ensemble de tous ces nombres est noté naturellement $\mathbb F_{117649}$, ce que l’on écrit plus souvent $\mathbb F_{7^6}$ (c’est à la fois plus court et probablement un peu plus parlant).
Tous les éléments de $\mathbb F_{7^6}$ vérifient $X^{7^6} = X$ (comme nous l’avons déjà signalé, la démonstration est identique à celle que nous avons donnée dans le cas de $\mathbb F_{49}$), ce qui montre qu’il y a encore des équations insolubles dans $\mathbb F_{7^6}$ (c’est par exemple le cas de l’équation $X^{7^6} = X+1$) et qu’on va devoir encore ajouter de nouveaux nombres. Et ceci ad vitam æternam car l’argument précédent s’appliquera toujours.
Le graphe des extensions de $\mathbb F_7$
On a jusqu’à présent construit $\mathbb F_7$ (c’est l’ensemble des colonnes), $\mathbb F_{49} = \mathbb F_{7^2}$ (obtenu en ajoutant $i$) et $\mathbb F_{7^6}$ (obtenu en ajoutant encore $j$)… et on a dit que cela n’allait pas s’arrêter là. Quels sont les exposants qui peuvent apparaître ? Voici la question que l’on se pose dans ce paragraphe.
En ajoutant uniquement $j$ et pas $i$, on obtient seulement $7^3$ nombres: ce sont ceux de la forme $A+Bj+Cj^2$ avec $A$, $B$ et $C$ dans $\mathbb F_7$. L’exposant $3$ est donc, lui aussi, présent.
En réalité, tous les exposants peuvent apparaître: pour construire $\mathbb F_{7^n}$, c’est-à-dire un ensemble de $7^n$ nombres sur lesquels les opérations usuelles sont définies, on peut s’inspirer du théorème 1. Celui-ci nous apprend que si un tel ensemble $\mathbb F_{7^n}$ existe, tous ses éléments doivent être solution de l’équation $X^{7^n} = X$. Or, par ailleurs, comme cette équation est de degré $7^n$, elle ne peut avoir plus de $7^n$ solutions. Ainsi $\mathbb F_{7^n}$ doit nécessairement être égal à l’ensemble des solutions de $X^{7^n} = X$.
Maintenant, pour construire effectivement $\mathbb F_{7^n}$, on renverse le raisonnement: on part de $\mathbb F_7$ et, par des méthodes analogues à celles utilisées pour ajouter $i$ et $j$ (que l’on ne souhaite pas détailler davantage dans cet article), on ajoute les unes après les autres toutes les solutions de l’équation $X^{7^n} = X$. Au final, l’ensemble obtenu compte $7^n$ éléments que l’on peut bien additionner, soustraire, multiplier et diviser (pour peu que le diviseur soit non nul). C’est exactement ce que l’on voulait.
Par ailleurs la caractérisation des éléments de $\mathbb F_{7^n}$ comme les solutions de l’équation $X^{7^n} = X$ a deux conséquences importantes :
- il n’y a qu’un seul ensemble de nombres (sur lequel les opérations usuelles sont définies) qui compte exactement $7^n$ éléments (et ceci, bien qu’{a priori} on puisse le construire par divers moyens [6]): ceci justifie qu’on le note $\mathbb F_{7^n}$ sans commentaire supplémentaire
- pour deux entiers $n$ et $m$, $\mathbb F_{7^n}$ est inclus dans $\mathbb F_{7^m}$ si et seulement si $n$ divise $m$.
Ce que l’on vient de dire est-il vraiment rigoureux ?
Bien que Galois élude complètement ce point dans son article (et ne dise donc en substance que ce que nous venons de mentionner ci-dessus), il est vrai qu’il apparaît à ce niveau un problème qui n’est pas évident à résoudre. En effet, tels que nous les avons construits, tous les $\mathbb F_{7^n}$ n’ont {a priori} aucun lien entre eux et ce n’est donc pas parce que tous les éléments de deux possibles $\mathbb F_{7^n}$ vérifient $X^{7^n} = X$ qu’ils sont forcément égaux. Pour que l’argument fonctionne, il faut encore montrer que partant de deux $\mathbb F_{7^n}$ {a priori} différents, disons $\mathbb F_{7^n}^{(1)}$ et $\mathbb F_{7^n}^{(2)}$, il existe un troisième ensemble de nombres $F$ qui les contient tous les deux et dans lequel on pourra raisonner. Cela peut effectivement se faire: typiquement, si $\mathbb F_{7^n}^{(1)}$ (resp. $\mathbb F_{7^n}^{(2)}$) est obtenu en ajoutant les nouveaux nombres $x_1, x_2, \ldots$ (resp. $y_1, y_2, \ldots$), on va prendre pour $F$ l’ensemble de nombres obtenu en ajoutant tous les $x_i$ et tous les $y_i$ (il s’agit juste ici de donner l’idée; la construction précise n’est pas aussi simple qu’il n’y paraît).
Dans l’approche moderne, pour éviter les soucis de ce type, on préfère souvent commencer par construire un très grand ensemble de nombres dans lequel on ajoute toutes les quantités possibles (on appelle cela une clôture algébrique) et travailler ensuite toujours à l’intérieur de celui-ci. Encore une fois, cela pose un certain nombre de problèmes techniques qui ne sont pas toujours faciles à résoudre de façon rigoureuse.
Le schéma suivant — que l’on appelle le graphe des extensions de $\mathbb F_7$ — montre comment tous ces $\mathbb F_{7^n}$ (enfin seulement les premiers) s’arrangent entre eux :
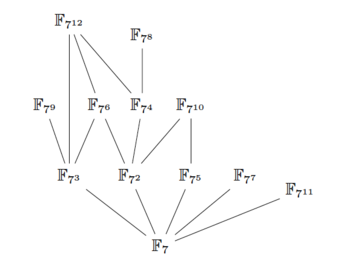
Ce n’est certes pas très simple, mais la logique sous-jacente n’est malgré tout pas très complexe puisqu’elle correspond à la divisibilité des entiers.
En tout cas, si l’on remplace $\mathbb F_7$ par $\mathbb Q$ (c’est-à-dire si l’on dessine le graphe des ensembles de nombres que l’on obtient en ajoutant à l’ensemble des nombres rationnels, les solutions des équations algébriques usuelles à coefficients rationnels), on obtient quelque chose de beaucoup plus compliqué que les mathématiciens sont encore loin de savoir entièrement décrire de nos jours. Comprendre la structure de ce graphe est, d’ailleurs, l’un des principaux enjeux actuels de l’arithmétique. De nombreux outils de toute sorte ont été développés pour y parvenir… et continuent de l’être !
Quelques applications des corps finis aujourd’hui
Mises à part la notation $\mathbb F_{7^n}$ qui est moderne, l’existence de $\mathbb F_{7^n}$ pour tout entier $n$ et la dernière remarque au sujet de l’inclusion les uns dans les autres des $\mathbb F_{7^n}$, tout ce que nous venons d’expliquer (et encore quelques autres choses) apparaît déjà dans l’article de Galois de 1830.
Depuis, bien sûr, la théorie a continué son chemin. Tout d’abord, des noms ont été donnés aux objets (ce qui arrive, en général, au moment où l’on commence à prendre véritablement conscience de leur importance). C’est ainsi qu’est apparue la notation $\mathbb F_{7^n}$ [7] et le terme corps fini qui désigne un ensemble fini de nombres sur lequel les opérations usuelles (addition, soustraction, multiplication, division) sont définies.
L’étude des corps finis a, de nos jours, de nombreuses applications dans différents domaines des mathématiques. Tout d’abord — et cela ne surprendra personne étant donnée la motivation d’origine — en arithmétique, en particulier en lien avec la résolution des équations diophantiennes ou, ce qui est très proche, avec la résolution des équations algébriques à coefficients rationnels. Ce problème est d’ailleurs étroitement lié à la compréhension du graphe des extensions de $\mathbb Q$, pour lequel les corps finis jouent un rôle essentiel: très grossièrement, l’idée est de chercher à l’intérieur du graphe des extensions de $\mathbb Q$ des parties qui ressemblent à celui des extensions de $\mathbb F_p$.
La cryptographie et la théorie des codes correcteurs d’erreurs utilisent, elles aussi, abondamment les corps finis. La cryptographie, on le sait, est la science du secret: c’est elle qui vous permet de communiquer confidentiellement avec tous vos interlocuteurs (par exemple avec votre banque, lorsque vous effectuez un achat) en empruntant néanmoins des canaux publics. La théorie des codes correcteurs d’erreurs est probablement moins connue, mais pourtant tout aussi importante — si ce n’est plus — dès que l’on souhaite communiquer ou stocker des données. Le problème qu’elle résout est celui de l’altération des données. Des interférences entre votre téléphone portable et l’antenne émettrice, une microrayure sur votre CD sont autant de facteurs qui peuvent endommager vos données. Pour retrouver, malgré tout, intact votre message téléphonique ou votre morceau de musique, l’idée que développe la théorie des codes correcteurs d’erreurs est de ne pas stocker ou transmettre vos données telles quelles, mais de les coder préalablement en ajoutant des redondances; si suffisamment peu d’altérations se produisent lors du transfert ou du stockage, les redondances ajoutées vont permettre de retrouver le message d’origine, sans aucune erreur. Les méthodes les plus efficaces pour effectuer ce codage utilisent les corps finis (en général les $\mathbb F_{2^n}$).
La théorie des corps finis s’immisce encore dans d’autres parties des mathématiques, par exemple la combinatoire. En effet, les tables d’addition ou de multiplication dans un corps fini possèdent des propriétés de symétrie tellement fortes qu’elles peuvent servir à construire des objets inattendus, et apparemment sans aucune relation avec les équations algébriques, comme certains carrés magiques ou des carrés gréco-latins, très utiles en statistique.
Notes
[1] Bien sûr, dans la langue courante, field veut dire champ tandis que corps se dit body. La terminologie est un peu malencontreuse de ce point de vue.
[2] Plus exactement, le petit théorème de Fermat ne fonctionne pas uniquement avec $7$ mais avec un nombre premier quelconque. Précisément, il affirme que pour tout nombre premier $p$ et tout entier $x$, la quantité $x^p−x$ est divisible par $p$ (ce qui revient à dire que, si on répartit les nombres en $p$ colonnes, alors $x^7$ est toujours dans la même colonne que $x$.
[3] Il est important ici d’avoir choisi un nombre de colonnes égal à $7$. Si on en avait choisi $5$, par exemple, $−\text{Col}(1)$ aurait eu une racine carrée qui aurait été $\text{Col}(2)$. Toutefois, on peut démontrer qu’avec n’importe quel nombre (premier) de colonnes, il existe toujours des nombres n’ayant pas de racine carrée ; par exemple, avec $5$ colonnes, la colonne de $3$ n’en a pas.
[4] Par exemple, $x = i + \text{Col}(2)$ n’a pas de racine carrée dans $\mathbb F_{49}$. Pour le démontrer (plus rapidement qu’en écrivant la table des carrés dans $\mathbb F_{49}$), on pourra calculer $x^{24}$ et obtenir une contradiction en supposant que $x$ s’écrit $y^2$.
[5] À nouveau, un moyen efficace de démontrer cela est de calculer $\text{Col}(2)^{16}$.
[6] Une conséquence de cela est que toute équation de la forme $X^2 + AX + B = 0$ avec $A, B \in \mathbb F_7$ a une solution dans le $\mathbb F_{49}$ que nous avons construit. L’exercice est laissé au lecteur.
[7] Et plus généralement $\mathbb F_{p^n}$ car, comme cela a été mentionné rapidement au début, tout le contenu de cet article s’étend au cas où l’on remplace $7$ par un nombre premier $p$ quelconque. Bien entendu, Galois travaillait déjà dans cette plus grande généralité. Nous avons choisi de nous limiter à $p=7$ pour cet article, simplement pour ne pas multiplier les notations et les éventuels problèmes.
 English
English  Français
Français 

