De l’ambiguité des puzzles aux idées de Galois

par X. Caruso et B. Teheux

Le but de cet article — accessible, nous l’espérons, au plus grand nombre, contrairement à ce que pourrait laisser penser la fin de cette phrase — est de présenter les idées générales de la théorie que Galois a développée pour déterminer si une équation algébrique était, oui ou non, résoluble par radicaux.

Sur l’ambiguité des puzzles

Pour l’instant, revenons à un vocabulaire plus courtois et introduisons le sujet de façon ludique par l’intermédiaire de deux petites énigmes logiques, qui prennent la forme de puzzles.

Deux puzzles pour commencer

Le degré 1

Voici le premier puzzle, dit de degré 1 (pour ceux qui ont déjà un peu fait des équations, l’analogie apparaîtra clairement plus tard) :

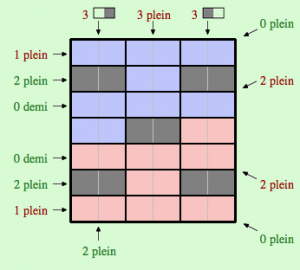
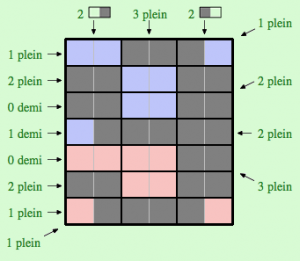
Pour ce jeu, vous disposez de 9 dominos « plein » et de 6 dominos « demi » (qui apparaissent sur le côté droit) que vous devez disposer sur la grille — en les déplaçant à l’aide de la souris — en respectant les contraintes (les flèches obliques indiquent des contraintes à respecter sur des diagonales). De plus, le nombre de dominos « plein » placés sur la zone rouge doit être égal à celui des dominos « plein » plaçés sur la zone bleue et il est en de même pour les dominos « demi ».
Pour vous aider, les indications apparaissent en rouge lorsqu’elles ne sont pas respectées et en vert lorsqu’elles le sont. De plus, un décompte des dominos « plein » et « demi » apparaît en bas à gauche.

Le degré 2

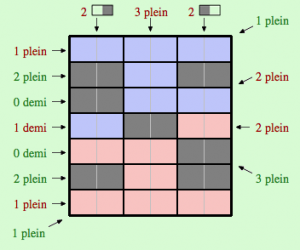
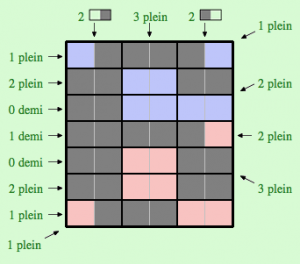
Voici maintenant la grille de degré 2 :

Les règles du jeux sont identiques, mais vous disposez cette fois de 11 dominos « plein » et de 4 dominos « demi » (et les contraintes sont évidement différentes).

La solution

Avant de continuer votre lecture, assurez-vous d’avoir tenté de résoudre les deux énigmes précédentes. En effet, vous tirerez largement plus de profit de la suite en ayant cherché un instant par vous-mêmes qu’en allant lire directement la solution.

Le degré 1

Commençons par indiquer un raisonnement — il n’est pas unique — qui permet de résoudre l’énigme de la grille de degré 1. Tout d’abord, notons qu’étant donné que les nombres de dominos « plein » sur les surfaces rouge et bleue doivent être identiques et vu qu’il y a un nombre impair de dominos « plein » en tout, la zone jaune est occupée par un domino « plein ». Nous pouvons ensuite exploiter les contraintes « 0 plein  » en diagonale pour placer les deux dominos « plein » sur la deuxième ligne et symétriquement, sur l’avant dernière ligne. Nous obtenons l’étape intermédiaire suivante.

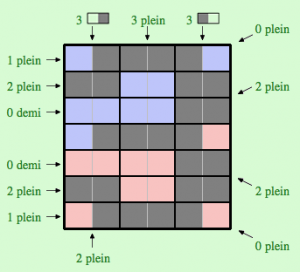
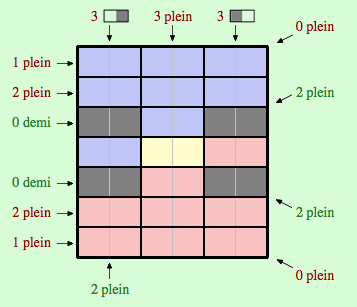
En utilisant à nouveau la contrainte « 0 plein », nous pouvons satisfaire les contraintes « 2 plein » en les diagonales de manière univoque. Ensuite, les contraintes « 0 demi » nous permettent de remplir la première et la dernière colonne avec les dominos « demi ». Cela nous permet de placer le domino « plein » sur la première et sur le dernière ligne. Nous avons donc une seule configuration possible comme solution, qui est représentée ci-dessous (et nous vérifions facilement qu’il s’agit bien d’une configuration qui satisfait l’ensemble des contraintes).

Ce puzzle est assez simple. Nous venons en effet d’expliciter un raisonnement qui mène à l’unique solution sans que le joueur se retrouve dans la situation de devoir faire un choix face à des alternatives qui respectent les contraintes (encore fallait-il trouver ce raisonnement). En effet, dans notre analyse du problème, en supposant que la solution existe, nous pouvons déterminer à chaque étape la position d’une des pièces de manière univoque.

Le degré 2

Pour débuter le deuxième puzzle, nous commençons par satisfaire la contrainte « 3 plein » sur la diagonale. Ensuite, en combinant la contrainte « 1 plein » sur la diagonale dans la zone bleue et la contrainte de la deuxième ligne, on peut remplir cette dernière. En procédant de manière symétrique pour l’avant dernière ligne, on obtient :

À ce stade, malheureusement, l’analyse de la situation ne nous permet plus de combiner les contraintes pour déterminer de manière univoque la position d’une pièce supplémentaire. Nous devons faire un choix pour placer la pièce suivante, ce qui correspond à faire une hypothèse sur la configuration de la solution que nous cherchons. Considérons par exemple le placement du deuxième domino « plein » sur la ligne du milieu. Nous avons deux possibilités et aucune des contraintes ne nous amène a priori à privilégier un de ces choix (sauf à envisager individuellement, comme nous allons le faire, les conséquences de ce choix sur le placement des pièces restantes).

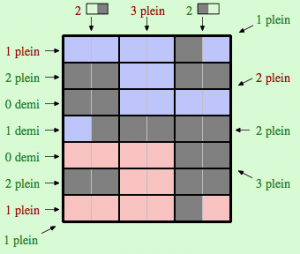
Choisissons de placer ce domino sur la zone rouge, tout en ne sachant pas, pour l’instant, si ce choix mène ou ne mène pas à une impasse. Une fois ce choix effectué, nous pouvons placer de manière univoque le domino « demi » sur la ligne du milieu ainsi que les deux dominos « demi » sur la dernière colonne. Nous obtenons :

Ensuite, nous pouvons compléter la colonne du milieu en tenant compte des contraintes de la première et de la dernière ligne. Enfin, en tenant compte du fait que les zones bleue et rouge doivent comporter le même nombre de dominos « plein », nous pouvons satisfaire la condition « 2 plein » sur la diagonale. Voici la configuration que nous obtenons, qui est effectivement une solution (toutes les contraintes sont satisfaites) :

L’hypothèse que nous avons posée à propos de la place du deuxième domino « plein » sur la ligne de milieu nous a donc mené à une solution. Que se serait-il passé si on avait fait l’autre choix ? Pour le savoir, remontons de quelques étapes et, au lieu de placer le domino « plein » sur la ligne du milieu dans la zone rouge, mettons-le dans la zone bleue. En poursuivant à partir de cette étape, par un raisonnement similaire au précédent, nous obtenons une deuxième solution :

Hormis le choix de la position du deuxième domino « plein » sur la ligne du milieu, les contraintes nous ont toujours dicté la position des dominos de manière univoque. Nous sommes donc certains qu’il n’y a que deux solutions (d’où le nom de degré 2).

Quelles leçons faut-il retenir de cela ?

Pour répondre à la question posée dans le titre, revenons un instant sur notre raisonnement en essayant de l’analyser.

Moins il y a de solutions, plus c’est facile

Pour la grille de degré 1 (qui admettait une seule solution), nous avons, à chaque étape, réussi à déduire des contraintes la position d’un nouveau domino, ce qui rendait le raisonnement plus simple.

Pour la grille de degré 2, au contraire, il n’en a pas été ainsi : rappelez-vous, à un moment, il a fallu choisir où placer le deuxième domino « plein » sur la ligne du milieu. Nous avons eu de la chance car, finalement, n’importe quel choix conduisait à une solution. Mais cela n’était pas garanti a priori et les lecteurs qui ont tenté de résoudre ce puzzle par eux-mêmes ont peut-être fait d’autres choix qui les ont conduits dans des impasses… comme, par exemple, celui de placer en première position le domino « plein » de la première ligne. En d’autres termes, l’apparente simplicité du raisonnement que nous avons présenté et qui mène aux deux solutions est une conséquence des choix judicieux que nous avons faits.

Était-il possible de résoudre la grille de degré 2 de façon systématique (c’est-à-dire de façon à ne jamais avoir à faire un choix) ? Non, évidemment : puisqu’il y a deux solutions, il faudra quoi qu’il arrive à un moment choisir entre l’une des deux ! Et faire ce choix sera toujours prendre le risque de se tromper et de s’engager dans une impasse !

Ainsi, la première leçon à retenir est que, plus le jeu a de solutions, plus il a des chances d’être difficile. Cela n’est pas entièrement intuitif car on pourrait imaginer à l’inverse que plus il y a de solutions, plus on va avoir de chance d’en trouver une. En réalité, ce n’est pas si simple : l’existence de plusieurs solution offre beaucoup de liberté et, en particulier, celle de s’engager dans des voies sans issue. Lorsque, à l’inverse, le chemin nous est dicté (c’est-à-dire lorsque la solution est unique), certes, on est nettement moins libre (c’est-à-dire qu’il n’y aura jamais aucun choix à faire) mais, au moins, on est certain d’arriver à bon port (c’est-à-dire de trouver la solution).

Comme autre illustration, prenez une grille de Sudoku (qui admet une unique solution) et imaginez maintenant que l’on efface un des numéros. La grille que l’on obtient admettra alors sans doute plus de solutions mais sera aussi certainement nettement plus compliquée, justement car l’on va devoir à un moment choisir quel numéro écrire dans la case effacée et il est peu probable que tous permettent d’aboutir.

Plus il y a de contraintes, plus c’est facile

C’est la deuxième leçon à retenir : plus il y a de contraintes, plus c’est facile. L’idée sous-jacente à cela est que lorsqu’il y a plus de contraintes, nous avons plus d’informations à notre disposition pour travailler, et le raisonnement sera par là-même simplifié.

Pour illustrer cette idée de la façon la plus parlante possible, imaginons la variante du puzzle de degré 1 suivante : la grille reste la même, les règles également sauf que l’on n’impose plus qu’il doit y avoir autant de dominos « plein » et « demi » dans les zones bleue et rouge. En d’autres mots, on supprime les couleurs sur la grille (et donc la contrainte liée aux couleurs)

Étant donné qu’il y a seulement une contrainte en moins, il est clair que la solution à laquelle nous sommes arrivés lorsque nous avons résolu la grille de degré 1 convient encore pour la variante que l’on vient de proposer (rien n’indique cependant qu’elle est unique). Autrement dit, il n’y a, semble-t-il, rien de plus à faire pour la résolution. Il semblerait donc que la seconde variante soit plus simple.

Mais, cette manière de comparer la complexité des énigmes ne tient pas ! En effet, elle est basée sur l’hypothèse qu’avant de s’arracher les cheveux sur la version « décolorée », on a déjà résolu la version « colorée ». Or, si l’on veut réellement comparer la difficulté des deux énigmes, il faut les attaquer à armes égales, c’est-à-dire en supposant ne rien savoir a priori sur la première version lorsque l’on commence la seconde. Et, dans ces conditions, tout est fort différent !

Pour nous en convaincre, rappelons simplement que, pour résoudre la première variante, nous avons commencé à raisonner ainsi : étant donné que le nombre de dominos « plein » sur les surfaces rouge et bleue doivent être identiques et vu qu’il y a un nombre impair de dominos « plein » en tout, la zone jaune est occupée par un domino « plein ». Ce raisonnement, clairement, ne peut plus être tenu pour la seconde variante puisque l’on n’a plus l’information concernant la répartition des dominos par couleur. Il semble donc que l’on soit bloqué dès le départ !

En fait, on peut s’en sortir et remplacer le raisonnement précédent par un autre — plus subtil, selon nous — qui permet d’arriver à la même conclusion. Le voici. Imaginons un instant qu’il n’y ait pas de dominos « plein » sur la case jaune. (Nous allons par la suite arriver à une impossibilité, ce qui montrera qu’il y a effectivement un domino « plein » sur cette case, c’est-à-dire ce que l’on voulait.) Avec cette supposition supplémentaire, il ne reste plus de choix pour la position de deux dominos « plein » dans chacune des deux diagonales centrales :

Mais alors, il nous reste 5 dominos « plein » à placer et il faudrait encore en mettre un sur la première ligne, deux sur la seconde, un sur l’avant-dernière et deux sur la dernière, c’est-à-dire 6 en tout. Manifestement, cela n’est pas possible, et on en conclut bien qu’il y a nécessairement un domino « plein » sur la case jaune.
Le raisonnement, ensuite, est identique à celui qui a été présenté pour la première variante. En effet, on pourra vérifier qu’il n’utilise plus jamais l’hypothèse d’« équirépartition selon les couleurs ».

Il est clair maintenant, nous l’espérons, qu’enlever une contrainte est de nature à compliquer l’énigme plutôt que la simplifier. À celles et ceux pour qui le deuxième raisonnement que l’on vient de donner (celui avec le décompte des dominos « plein ») semble plus simple que le premier (celui avec l’argument de parité), disons simplement que, dans la première variante de l’énigme (c’est-à-dire celle possédant la contrainte supplémentaire), on pouvait au choix mener l’un ou l’autre des raisonnements. Dans la seconde variante, au contraire, le premier n’est plus possible.

Utilisation des symétries

Imaginons une grille bien plus complexe qui rendrait un raisonnement analytique (comme celui qui nous a mené aux solutions des énigmes précédentes) difficile, voir impraticable. Quels autres outils avons-nous à disposition pour tenter de résoudre les énigmes ? Montrons que la notion de symétrie peut nous aider.

Le degré 1 « décoloré »

Nous constatons que la grille de l’énigme de degré 1, dans sa version « décolorée » (c’est-à-dire où l’on a supprimé la contrainte sur les couleurs), possède une symétrie « miroir haut-bas » : si nous considérons l’image miroir de la grille et de ses contraintes par rapport à la ligne du milieu, nous obtenons exactement la même grille et les mêmes contraintes. (Notez bien que la version initiale ne possède pas cette propriété car les couleurs sont modifiées — et pas uniquement échangées — par la symétrie.)

Nous en concluons que si nous obtenons une solution, nous pouvons en obtenir une autre en appliquant à notre configuration solution la transformation « miroir haut-bas ». Les solutions apparaissent donc par paires, sauf si elles sont invariantes pour cette transformation, ce qui est le cas de la solution que nous avons trouvée.

Si l’auteur de l’énigme nous donne un indice sur le problème et nous indique qu’il n’existe qu’une seule solution, cela nous permet donc de déduire que cette unique solution est nécessairement symétrique (puisque les solutions qui ne le sont pas vont par deux). Or, savoir à l’avance que la solution est symétrique est un indice de taille ! Par exemple, dans notre recherche de solution, chaque fois que nous plaçons un domino dans une des demi-grilles « haut&nbsp» ou « bas », nous pouvons en placer un second symétriquement au premier dans l’autre demi-grille, ce qui nous permet d’avancer deux fois plus vite…

Le degré 2

Bien qu’elle ne saute pas aux yeux, la grille de l’énigme de degré 2 ne change pas lorsque l’on tourne la feuille d’un demi-tour (on parle de symétrie centrale). Comme tout à l’heure, les solutions vont donc par paires, sauf si elles sont invariantes par demi-tour. Les deux solutions que nous avons trouvées forment une de ces paires : à partir d’une des deux solutions, on peut obtenir l’autre en la faisant tourner un demi-tour. En particulier, après avoir trouvé la première solution, nous aurions pu obtenir directement la seconde et également conclure, dès ce moment, qu’il ne pouvait y en avoir d’autres. En effet, puisque le choix de placer le domino dans la zone rouge nous a conduit à une solution et une seule, il est clair que l’on aurait également obtenu une solution en une seule en le plaçant dans la zone bleue puisque cela revient in fine à tourner la feuille et donc à résoudre la même énigme.

Mieux encore : en supposant que l’énigme possède au moins une solution, nous pouvions utiliser la symétrie pour nous alléger l’esprit face au dilemme « Vais-je placer le deuxième domino « plein » sur la ligne du milieu dans la zone rouge ou dans la zone bleue ? » En effet comme, par symétrie, les deux choix se correspondent, aucun ne peut mener à une impasse car, sinon, les deux y mèneraient et il n’y aurait au final aucune solution.

Le jeu des équations algébriques

Dans cette deuxième partie, nous étudions un nouveau jeu, un peu moins visuel certes, mais qui nous conduira directement aux travaux de Galois.

Sauras-tu retrouver notre âge ?

Il était une fois, deux brillants mathématiciens — appelons-les Xavier et Bruno — qui, après une longue discussion en étaient venus à se demander lequel des deux était le plus jeune. Au même moment, un collègue à eux, Martin, passe non loin de là et entend « Ah, ah, donc c’est moi le plus jeune ! ». Intrigué, il s’approche, découvre Bruno et Xavier en train de discuter et, se souvenant de ce qu’il a entendu il y a une minute, leur demande leur âge respectif.

Mais les deux mathématiciens sont joueurs, et ils ne dévoilent à Martin que la somme et le produit de leurs âges : la somme fait 61 et le produit 930. Martin peut-il alors retrouver l’âge de ses deux amis ?
La réponse est que cela dépend… Plus précisément, comme Martin est lui aussi mathématicien, ce qu’il sait faire (et qui est expliqué ci-après, en petit, pour nos lecteurs), c’est retrouver les deux âges en résolvant une équation : ici, il trouve 30 et 31 ans. Par contre, ce qu’il ne peut pas faire, c’est savoir à qui il doit attribuer ces âges (car si on intervertit les deux âges, évidemment, la somme et le produit restent inchangés)… à moins, bien entendu, qu’il ait reconnu la voix de celui qui s’est exclamé être le plus jeune !

Si $x$ et $y$ sont les deux âges que l’on cherche, on a les équations $x+y = 61$ et $xy = 930$. En remplaçant $y$ par $61-x$ dans la deuxième équation, on obtient $x(61-x) = 930$, c’est-à-dire $x^2 – 61 x + 930 = 0$. On résout cette équation par exemple en calculant le discriminant et en appliquant les formules, et on trouve les solutions $x=30$ et $x=31$.

Nous sommes donc en présence d’une énigme ayant deux solutions : soit Bruno a 30 ans et Xavier 31, soit c’est le contraire. Et, sans information supplémentaire, on ne peut rien dire de plus. D’après les idées générales qui ont été présentées dans la première partie de cet article, cette ambiguité est de nature à accentuer la difficulté de résolution de l’énigme.

Un jeu qui se joue aussi en famille

Ce petit jeu des âges peut se rejouer avec plus de monde, par exemple en famille. Imaginons que trois sœurs cherchent à faire redécouvrir leur âge (ou, plus généralement, n’importe quel nombre de leur choix) à leur grand-mère qui commence un peu à tout mélanger, à l’exception de ses cours de mathématiques de jeunesse.

Lorsqu’il y a trois protagonistes, il ne suffit plus d’annoncer la somme et le produit des âges, mais il faut également une information supplémentaire qui peut être, par exemple, la somme des produits des âges deux à deux. Cela signifie que chaque fille multiplie entre eux les âges de ses deux sœurs et qu’elles communiquent à la grand-mère la somme des trois résultats obtenus — ainsi que, comme précédemment, la somme et le produit des trois âges.

Avec toutes ces informations en main, la grand-mère qui n’a pas oublié ses cours avancés de mathématiques, arrive à retrouver les trois âges mais, encore une fois, elle ne sait pas a priori quel âge correspond à quelle fille. S’il n’est pas si facile d’expliquer comment retrouver les âges (il s’agit en fait de résoudre une équation de degré 3), il est nettement plus aisé de comprendre que, sans information supplémentaire, on ne va pouvoir attribuer à coup sûr correctement chaque âge à chaque fille. En effet, si l’on permute les âges entre les filles, la somme et le produit demeurent inchangés, de même en fait que la somme des produits des âges deux à deux.

Ainsi, si la grand-mère ne se souvient plus qui, parmi ses petites-filles, est l’aînée, la cadette et la benjamine, il lui restera six possibilités : si les filles s’appellent Émilie, Sofia et Emmy, ces six possibilités correspondent aux six façons que l’on a de les ordonner par âge décroissant (de l’aînée à la plus jeune) :

1. Emmy, Sofia, Émilie
2. Emmy, Émilie, Sofia
3. Sofia, Émilie, Emmy
4. Sofia, Emmy, Émilie
5. Émilie, Emmy, Sofia
6. Émilie, Sofia, Emmy

Comment peut-on calculer qu’il y a bien $6$ possibilités ? C’est assez simple : il suffit de se dire que l’on a $3$ possibilités pour l’aînée, mais une fois que ce choix est fait, on a plus que $2$ possibilités pour la deuxième et, finalement, plus qu’une seule pour la petite dernière. L’opération à faire est donc $3 \times 2 \times 1$, ce qui fait bien $6$.

Le même jeu peut encore se jouer à quatre, cinq et même autant qu’on veut. Si l’on joue à $n$, les informations à donner sont la somme des nombres choisis (les âges si l’on veut), la somme de leurs produits deux à deux, la somme de leurs produits trois à trois, et ainsi de suite jusqu’à la somme de leurs produits $n$ à $n$ (ce qui est le produit étant donné qu’il y a un unique produit $n$ à $n$). Retrouver les nombres à partir de ces informations revient alors à résoudre une équation de degré $n$ [1] et il y a, à la fin, $1 \times 2 \times 3 \times \cdots \times n$ façons de redistribuer les nombres parmi les joueurs. Pour quatre nombres, cela fait $24$ possibilités ; pour cinq, cela en fait $120$ ; pour six, $720$, etc. On voit donc que cela grandit très vite.

Imposer des contraintes supplémentaires

Comme on vient de le dire, lorsque le nombre de joueurs augmente, le nombre de possibilités augmente très rapidement et, selon la philosophie générale de la première partie, avec lui, la difficulté à résoudre l’énigme.

L’idée principale sur laquelle reposent les travaux de Galois peut se résumer comme suit : pour simplifier le problème, on va imposer des contraintes supplémentaires qui vont faire diminuer le nombre de solutions. Bien sûr, ces contraintes ne peuvent pas être n’importe lesquelles car l’on souhaite, au minimum, qu’il reste des solutions. Mais dès qu’il en reste une, on est sauvé car on pourra retrouver les autres simplement en redistribuant les nombres.

Un exemple sera certainement plus parlant qu’un long discours. Imaginons donc que quatre personnes — que l’on prénommera Sandrine, Sébastien, Natacha et David — choisissent chacune un nombre et nous dévoilent la somme de ces quatre nombres, la somme des produits deux à deux, etc.

Plaçons-nous dans le cas où aussi bien pour la somme des nombres que pour la somme des produits trois à trois, la valeur dévoilée soit 0. Certainement, il y a alors parmi les nombres choisis des nombres négatifs et, en fait, en revenant aux équations algébriques, on peut démontrer que si un nombre a été choisi, alors son opposé (c’est-à-dire le même nombre où le signe a été modifié) a lui aussi été choisi [2]. En particulier, quelqu’un a choisi un nombre qui est l’opposé de celui de Sandrine. Certes, on ne sait pas a priori de qui il s’agit, mais cela permet malgré tout de couper le problème en trois :

1er cas : Sandrine et Natacha ont choisi des nombres opposés
2ème cas : Sandrine et Sébastien ont choisi des nombres opposés
3ème cas : Sandrine et David ont choisi des nombres opposés

Il y avait initialement 24 possibilités en tout, mais maintenant, si l’on résout l’équation cas par cas, il n’y a plus que 8 possibilités à chaque fois. On a donc, comme cela, simplifié le problème.

Par ailleurs, on se doute déjà que si l’on arrive à résoudre le premier cas, on saura également résoudre les deux autres : pour le deuxième, par exemple, il suffira d’échanger les rôles de Sébastien et Natacha partout dans la solution. Ainsi, il suffit de résoudre le problème dans le premier cas, c’est-à-dire en s’imposant la contrainte supplémentaire suivante :

Sandrine et Natacha ont choisi des nombres opposés.

De ce fait, comme on l’a déjà dit, on réduit de 24 à 8 le nombre de solutions, et on simplifie d’autant la résolution du problème. Ces 8 solutions se décrivent comme suit : on peut échanger les nombres de Sandrine et de Natacha, on peut échanger les nombres de Sébastien et de David, et on peut aussi finalement échanger globalement les nombres des garçons avec ceux des filles. Par exemple, si les nombres choisis sont $1$, $-1$, $2$ et $-2$, les huit possibilités sont :

$$\begin{array}{c|c|c|c}
\text{Sandrine} &
\text{Natacha} &
\text{Sébastien} &
\text{David} \\
\hline
1 & -1 & 2 & -2 \\
-1 & 1 & 2 & -2 \\
1 & -1 & -2 & 2 \\
-1 & 1 & -2 & 2 \\
2 & -2 & 1 & -1 \\
-2 & 2 & 1 & -1 \\
2 & -2 & -1 & 1 \\
-2 & 2 & -1 & 1
\end{array}$$

les autres permutations étant exclues car elles ne respectent pas la contrainte supplémentaire.

De façon générale, Galois s’intéresse de façon systématique à ces contraintes supplémentaires que l’on est en mesure d’imposer a priori pour le jeu précédent — qui est, soulignons-le bien, celui de la résolution des équations algébriques et donc pas aussi anodin que la présentation qu’on en a faite pourrait le laisser croire. Il s’intéresse encore plus particulièrement aux solutions qu’il reste après avoir imposé toutes ces contraintes (il peut, dans certains cas, y avoir plusieurs contraintes… et, dans d’autres cas, aucune). Cet ensemble de solutions est ce que Galois appelle le groupe de l’équation [3], et ce que l’on appelle aujourd’hui le groupe de Galois de l’équation.

Mine de rien, ce que l’on vient d’expliquer, avec Sandrine, Natacha, Sébastien et David qui jouaient à cacher des nombres, n’est rien d’autre que le calcul du groupe de Galois de l’équation bicarrée générique… Impressionnant, n’est-ce pas ?

Ce n’est pas la taille qui compte !

On a dit précédemment qu’au plus une énigme possédait de solutions, au plus celle-ci était difficile à résoudre. En réalité, les choses sont un peu plus subtiles que cela. Pour nous en rendre compte, imaginons que l’on soit en présence de 10 jeux différents qui possèdent chacun deux solutions. Si l’on considère ces jeux comme un unique jeu (avec 10 étapes si l’on veut), il va admettre $2^{10} = 1024$ solutions, ce qui est énorme. Pourtant, évidemment, résoudre ce jeu en 10 étapes n’est pas plus difficile que résoudre chaque petit jeu individuellement… et chacun de ces petits jeux n’avaient pas l’air si ardu puisqu’il avait seulement 2 solutions.

Ce qui se passe — et que Galois avait très bien remarqué — c’est qu’il ne suffit pas de compter le nombre de solutions, mais il faut encore comprendre comment celles-ci s’agencent entre elles. Dans l’exemple du jeu en 10 étapes, les 1024 solutions pouvaient toutes se construire à partir de 10 blocs de 2 solutions, et cela rendait ce grand ensemble de 1024 solutions pas aussi méchant qu’il en avait l’air à première vue.

Galois arrive à donner un sens précis et général (c’est-à-dire valable pour tout groupe de solutions) à cette notion de « décomposabilité ». Nous n’allons pas l’expliquer dans tous les détails, mais tenter de donner quelques éléments permettant au lecteur de l’appréhender. La première chose à faire, pour cela, est de réinterpréter le groupe de Galois en termes de symétries. Rappelez-vous : nous avons vu dans la première partie que l’étude des symétries pouvait apporter une aide précieuse pour la résolution des puzzles. Ici, elle s’avère également être d’une efficacité redoutable.

Entrée en scène des symétries

Bien entendu, dans le cas du jeu des équations, une symétrie n’est certainement pas un demi-tour de la feuille ou quelque chose de ce genre, cela n’aurait aucun sens. Il s’agit plutôt d’une redistribution des nombres parmi les joueurs. Voici quelques exemples de symétries dans le cas du jeu avec Sandrine, Sébastien, Natacha et David :

• Sandrine et David échangent leurs deux nombres,
• David donne son nombre à Sébastien, Sébastien donne le sien à Natacha, et enfin Natacha donne le sien à David,
• les garçons échangent leur nombre entre eux, et les filles font de même.

Comme nous l’avons déjà expliqué dans la première partie, ces symétries peuvent être utilisées pour produire de nouvelles solutions à partir d’anciennes. La situation est encore meilleure dans le cas du jeu des équations puisque dès que l’on connaît une solution, il est possible de les obtenir toutes simplement en appliquant des symétries.

Lorsque, comme Galois, on ajoute des contraintes supplémentaires (du type Sandrine et Natacha ont choisi des nombres opposés), le nombre de symétries diminue. Le groupe de Galois de l’équation peut être également défini comme l’ensemble des symétries qu’il reste une fois que toutes les contraintes ont été ajoutées. Cet ensemble est, en effet, exactement [4] le même que celui des solutions possibles (après ajout des contraintes également) puisque l’on a dit que toute solution pouvait s’obtenir en appliquant une symétrie (nécessairement unique) à une solution « initiale » fixée [5].

L’avantage de considérer des symétries plutôt que des solutions est que celles-ci peuvent se composer : si l’on a deux symétries, on peut appliquer la première d’entre elles, puis la seconde, cela donne encore une symétrie que l’on appelle la composée des deux. Bien qu’il ne s’agisse pas d’un groupe de Galois, reprenons, pour bien comprendre cette notion, l’exemple du grand jeu formé de 10 petits jeux possédant chacun deux solutions. Supposons en outre, pour fixer les idées, que chaque petit jeu soit une grille à remplir possédant deux solutions qui s’échangent par un demi-tour (comme c’était le cas pour la grille de degré 2 présentée dans la première partie de cet article). Le grand jeu a alors 1024 symétries : en effet, pour chacun des 10 petits jeux, on peut choisir soit de tourner la grille correspondante d’un demi-tour, soit de la laisser comme elle est. Chacune de ces symétries peut-être représentée par une suite de dix symboles comme suit :

$$\begin{array}{c}
\curvearrowleft & \cdot & \cdot & \cdot & \cdot & \cdot & \curvearrowleft & \cdot & \cdot & \cdot
\end{array}$$

où un symbole $\curvearrowleft$ placé en i-ième position signifie que l’on fait tourner la i-ième grille alors qu’un symbole $\cdot$ signifie que l’on n’a rien fait. La suite de symboles précédente signifie donc que seules les grilles numérotées 1 et 7 ont été retournées. Par ailleurs, la composition des symétries peut se lire directement sur les listes de symboles : par exemple la composée des deux listes ci-dessous

$$\begin{array}{c}
\curvearrowleft & \cdot & \cdot & \cdot & \cdot & \cdot & \curvearrowleft & \cdot & \cdot & \cdot \\
\curvearrowleft & \curvearrowleft & \cdot & \curvearrowleft & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\
\end{array}$$

est

$$\begin{array}{c}
\cdot & \curvearrowleft & \cdot & \curvearrowleft & \cdot & \cdot & \curvearrowleft & \cdot & \cdot & \cdot
\end{array}$$

puisque, bien sûr, deux demi-tours successifs s’annulent.

Jeux auxiliaires et sous-groupes distingués

Continuons à travailler avec le même exemple et concentrons-nous un instant sur l’ensemble des symétries qui ne modifient pas le premier sous-jeu : ce sont évidemment, par définition, celles dont le premier symbole du codage est un $\cdot$. Lorsque l’on compose deux telles symétries, la symétrie que l’on obtient est encore du même type. C’est évident avec la notation symbolique, mais ça l’est également sans elle : si on applique une première symétrie qui ne touche pas au premier sous-jeu puis une seconde qui ne touche pas non plus à ce premier sous-jeu, il est clair qu’au final le premier sous-jeu n’aura pas été touché.

Cette propriété que l’on vient de mettre en valeur est donc vraie de façon bien plus générale : si un jeu ayant autant de symétries que de solutions (typiquement le jeu des équations algébriques) peut se décomposer à l’aide d’un jeu auxiliaire, nécessairement son groupe de symétries doit posséder un sous-ensemble stable par composition qui est exactement l’ensemble des symétries ne touchant pas au jeu auxiliaire.
Ce sous-ensemble possède une propriété supplémentaire plus subtile : si on applique d’abord n’importe quelle symétrie, puis une symétrie du sous-ensemble, puis que l’on défait la première symétrie, alors le résultat doit rester dans l’ensemble. En effet, regardons ce qui s’est passé sur le jeu auxiliaire : premièrement, on a appliqué une certaine symétrie, ensuite, on n’a rien fait (puisque, justement, on a appliqué une symétrie dans le sous-ensemble qui ne touche pas à ce jeu) et enfin, on a défait la première symétrie ; au final, on n’a donc rien fait !

Un sous-ensemble stable par composition et vérifiant en outre la propriété supplémentaire que l’on vient de mettre en lumière est ce que l’on appelle un sous-groupe distingué. On vient d’expliquer que, lorsqu’un jeu peut se décomposer à l’aide d’un jeu auxiliaire, son groupe de symétries admet nécessairement un sous-groupe distingué. Galois démontre la réciproque dans le cas du jeu des équations algébriques : si le groupe d’un tel jeu admet un sous-groupe distingué, alors ce jeu peut s’attaquer à l’aide d’un jeu auxiliaire (qui est encore un jeu d’équations algébriques) pour lequel le nombre de solutions (ou, cela revient au même, de symétries) — c’est-à-dire le groupe de Galois — est plus petit.
En termes d’équations algébriques cela se reformule comme suit : si le groupe d’une équation algébrique admet un sous-groupe distingué, alors cette équation peut s’attaquer à l’aide d’une équation auxiliaire ayant un plus petit groupe de Galois. Attention, toutefois, cette équation auxiliaire n’a pas nécessairement un degré inférieur !

Ainsi, en étudiant uniquement le groupe de Galois, ses sous-groupes distingués (et éventuellement les sous-groupes distingués de ses sous-groupes distingués, etc.), on peut déterminer si l’équation est résoluble (en s’autorisant un certain nombre d’outils fixés à l’avance, à savoir les opérations usuelles et l’extraction des racines [6]) : si c’est le cas, on dit que le groupe lui-même est résoluble, sinon on dit qu’il ne l’est pas.
Si l’équation est de degré inférieur ou égal à 4 — c’est-à-dire, s’il y a au plus quatre joueurs qui ont choisi un nombre — le groupe que l’on obtient est toujours résoluble (même s’il contient le nombre maximum de symétries, à savoir 24). Cela rend compte du fait que toutes ces équations sont résolubles. Par contre, à partir du degré 5 — c’est-à-dire, à partir de cinq nombres choisis — on obtient en général des groupes non résolubles et donc des équations également non résolubles.

Notes

[1] Pour ceux qui sont intéressés, si $s_k$ désigne la somme des produits $k$ à $k$, l’équation à résoudre est :

$$x^n – s_1 x^{n-1} + s_2 x^{n-2} – s_3 x^{n-3} + \cdots + (-1)^n s_n = 0.$$

[2] En effet, d’après la note de bas de page précédente, les nombres choisis sont solutions de l’équation $x^4 + s_2 x^2 + s_4 = 0$ puisque l’on sait que $s_1$ et $s_3$ sont nuls. À partir de là, on voit que si $x$ est solution, alors il en est de même de $-x$ (puisque $(-x)^2 = x^2$ et $(-x)^4 = x^4$).

[3] Dans notre présentation, il faudrait peut-être plutôt dire le « le groupe du jeu »…

[4] Il y a une hypothèse implicite pour avoir l’identification entre ensemble de solutions et ensemble de symétries : il faut supposer qu’aucun nombre n’a été choisi indépendamment par deux joueurs différents. En effet, si par exemple Sandrine et Sébastien ont choisi le même nombre, la symétrie qui échange ses deux personnages ne modifie pas la distribution des nombres. Dans ce cas particulier — que nous supposerons ne pas se produire dans la suite de la discussion — il y a donc moins de solutions que de symétries.
On remarquera que l’on a déjà rencontré l’analogue du « nombre qui apparaît deux fois » (dans la théorie des équations algébriques, on utilise le terme de racine double) avec l’exemple du puzzle de degré 1 « décoloré ». En effet, celui-ci admettait bien une symétrie, mais celle-ci ne modifiait pas la solution… qui donc, en ce sens, pourrait être qualifiée de solution double.

[5] Sous l’hypothèse expliquée dans la note ci-dessus, l’ensemble de solutions s’identifie effectivement à l’ensemble de permutations mais il faut quand même rester prudent car cette identification dépend du choix d’une solution privilégiée ; il y a donc plusieurs identifications possibles (dès qu’il y a plusieurs solutions) et il est généralement important, lorsque l’on souhaite raisonner, d’être certain de celle dont on parle.
En réalité, le « vrai » groupe de Galois est bel et bien l’ensemble des symétries. L’ensemble des solutions est ce que l’on appelle, en termes modernes, un torseur sous le groupe de Galois. Dans les textes de Galois, cette distinction apparaît aussi : le mot permutation est employé pour ce qui est appelé ici symétrie, tandis que c’est le mot substitution qui est utilisé pour ce que l’on a appelé ici solution. Galois comprend — peut-être le premier — qu’il est vraiment important de passer des substitutions aux permutations. Cependant, ces deux notions ne sont pas rigoureusement définies dans ses textes et, selon les auteurs de cet article, il n’insiste pas toujours autant qu’il le faudrait (au moins avec le recul que l’on a actuellement) sur l’intérêt ou la nécessité de travailler avec l’une plutôt qu’avec l’autre.

[6] D’un point de vue de jeux, cela revient à dire que l’on convient que l’on sait résoudre certains jeux particuliers qui sont ceux pour lesquels toutes les quantités annoncées sont 0 hormis éventuellement le produit.