À propos de l’image du mug… | Bicentenaire Galois

par X. Caruso

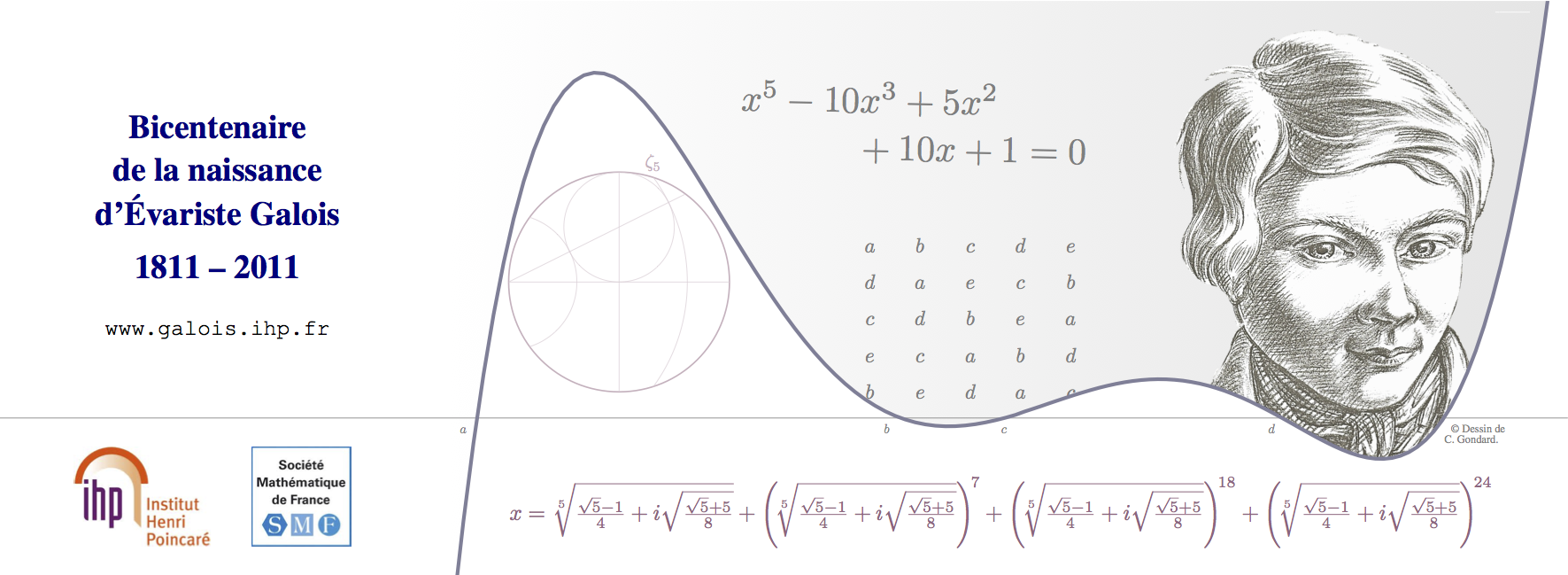
Lors du colloque et de l’après-midi grand public, des mugs ont été distribués aux participants. Sur ceux-ci était imprimée l’image suivante (conçue pour l’occasion par l’auteur de cet article),

au sujet de laquelle quelques explications sont certainement nécessaires. L’objet de cet article est de les donner. Pour la lecture de la suite, une connaissance des nombres complexes est requise.

Décorticage des divers éléments de l’image

Passons rapidement sur la mention du bicentenaire de la naissance d’Évariste Galois sur la partie gauche, ainsi que sur celle du site web et des logos : tout le monde aura compris ce que cela signifie sans explication supplémentaire. Pareillement, attardons-nous guère sur le portrait de Galois à droite. Mentionnons toutefois qu’il a été réalisé pour l’occasion par Claude Gondard et ne se veut pas particulièrement fidèle à la réalité. Il a été imaginé par l’auteur à partir des autres portraits que nous avons, peu nombreux.

En haut de la partie grisée, on voit apparaître l’équation algébrique de degré 5 (que l’on appellera, en reprenant les termes de Galois, l’équation proposée ou, encore plus simplement, la proposée) $x^5 – 10 x^3 + 5x^2 + 10x + 1 = 0$. La courbe bleue représente le graphe de la fonction polynomiale $f : x \mapsto x^5 – 10 x^3 + 5x^2 + 10x + 1$ tandis que la ligne horizontale qui traverse l’image de part en part n’est autre que l’axe des abscisses. Ses points d’intersection avec la courbe correspondent donc aux solutions de l’équation $f(x) = 0$, c’est-à-dire de la proposée. Si l’on regarde attentivement l’image, on voit que les quatre premières intersections sont marquées — en tout petit — par les lettres $a$, $b$, $c$ et $d$. Par manque de place, la lettre $e$ n’a pas été indiquée aux côtés de la dernière intersection ; toutefois, bien entendu, il faut faire comme si elle était là. Bref, les lettres $a$, $b$, $c$, $d$ et $e$ désignent les cinq solutions de l’équation proposée.

Le petit tableau qui apparaît juste au-dessous de la proposée représente son groupe de Galois. Chaque élément de ce groupe est donné par une ligne du tableau qui représente une permutation des cinq lettres $a$, $b$, $c$, $d$, $e$ (c’est-à-dire des cinq solutions de l’équation). Comme le tableau compte 5 lignes, il y a 5 éléments dans le groupe de Galois ; il est donc particulièrement petit, sachant qu’une équation de degré 5 peut avoir un groupe de Galois comptant jusqu’à 120 éléments (qui sont les 120 permutations possibles de ses solutions). Cette petitesse du groupe reflète le fait que l’équation proposée est résoluble par radicaux… alors qu’en général, une équation de degré 5 ne l’est pas, comme l’a démontré Abel.

Au-dessous de la ligne horizontale (l’axe des abscisses) apparaît d’ailleurs la solution de cette équation. On peut se demander pourquoi il y a une unique formule alors que nous avons dit que l’équation admet 5 solutions. Le fait est que cette unique formule permet de former, à elle seule, les 5 solutions. En effet, si l’on examine un instant, on se rend compte qu’elle prend la forme :

$$x = \zeta_{25} + (\zeta_{25})^7 + (\zeta_{25})^{18} + (\zeta_{25})^{24}$$

avec $\zeta_{25} = \sqrt[5]{\zeta_5}$ et $\zeta_5 = \frac{\sqrt 5 – 1} 4 + i \sqrt{\frac{\sqrt 5 + 5} 8}$. Les symbôles $\zeta_5$ et $\zeta_{25}$ se lisent respectivement zêta-5 et zêta-25.

Telle qu’on l’a écrite, la valeur de $\zeta_5$ n’est probablement pas très parlante, mais il se trouve qu’elle est pourtant assez simple car $\frac{\sqrt 5 – 1} 4$ n’est autre que le cosinus de $\frac{2\pi} 5$ alors que $\sqrt{\frac{\sqrt 5 + 5} 8}$ en est le sinus. Ainsi, par les formules de Moivre, $\zeta_5 = e^{2i\pi/5}$ : c’est une racine 5-ième de l’unité.

Le nombre $\zeta_{25}$, qui est défini comme une racine 5-ième de $\zeta_5$, est donc une racine 25-ième de l’unité : on a $(\zeta_{25})^{25} = 1$. Contrairement à $\zeta_5$, il n’est toutefois pas exactement défini puisque, comme tous les nombres non nuls, $\zeta_5$ admet 5 racines 5-ièmes dans $\mathbb C$. Précisément, on a :

$$\zeta_{25} = \text{exp}\:\Big(\frac{2i\pi}{25} + \frac{2ik\pi}{5}\Big)$$

où $k$ peut prendre les valeurs $0$, $1$, $2$, $3$ et $4$. Le nombre $x$ qui valait $\zeta_{25} + (\zeta_{25})^7 + (\zeta_{25})^{18} + (\zeta_{25})^{24}$ peut donc prendre lui aussi a priori 5 valeurs selon la détermination que l’on choisit pour $\zeta_{25}$. C’est en effet exactement ce qui se passe :

pour $k = 0$, on trouve $x = d$,
pour $k = 1$, on trouve $x = b$,
pour $k = 2$, on trouve $x = c$,
pour $k = 3$, on trouve $x = a$,
pour $k = 4$, on trouve $x = e$.

L’unique formule écrite sur l’image du mug définit donc bien les cinq solutions. Il faut toutefois faire attention à quelque chose : pour obtenir bel et bien une solution, il est tout à fait important de choisir la même détermination de $\zeta_{25}$ pour chacune des quatre occurrences dans l’expression donnant la valeur de $x$ ! Si l’on ne prend pas cette précaution, la valeur que l’on obtiendra au final ne sera généralement pas solution de la proposée.

Enfin, la figure géométrique qui apparaît dans la « bosse » de la fonction représente une construction du polygone régulier à 5 côtés et fait apparaître le nombre complexe $\zeta_5$ (ou plutôt le point du plan ayant cette affixe) qui a été joué un rôle important dans l’explication précédente.

Comment construit-on une équation résoluble ?

Les travaux d’Abel puis de Galois montrent que, généralement, les solutions d’une équation de degré 5 ne peuvent pas s’écrire à l’aide de formules ne faisant intervenir que les quatre opérations usuelles (addition, soustraction, multiplication, division) et des extraction de racines ($\sqrt{\phantom{X}}$, $\sqrt[3]{\phantom{X}}$, $\sqrt[4]{\phantom{X}}$, etc.). Cependant, comme on l’a vu avec l’équation du mug, il y a des cas où cette résolution est possible. Comment peut-on trouver de tels exemples ?

Pour fabriquer une équation résoluble, une approche consiste à « renverser » le problème : on commence par choisir un nombre qui s’exprime à l’aide des opérations usuelles et des extractions de racines, puis on cherche une équation dont il est solution. Toutefois, pour obtenir par cette voie des exemples à la fois intéressants et « pas trop gros » (c’est-à-dire de degré raisonnable et ne faisant pas intervenir des coefficients trop compliqués), un peu de réflexion préalable n’est pas inutile.

Trouver des exemples sans fioriture n’est pas difficile : typiquement, on peut choisir $\sqrt[5]{2}$ pour la solution et l’équation qui correspond est alors $x^5 – 2 = 0$. Cela fonctionne, en effet, mais reste quand même pas véritablement impressionnant. Pour obtenir des exemples plus élaborés, on a envie de commencer par choisir une expression plus complexe, par exemple (déjà sans aller très loin) :

$$x = \sqrt[3]{3} + \sqrt[5]{5}.$$

Le problème devient alors de trouver une équation dont ce nombre est solution… et cela n’est pas facile du tout [1]. Pour donner une idée de la complexité de la chose, contenons-nous de donner l’équation de plus petit degré dont est solution le $x$ que l’on a choisi ; c’est

$$\begin{array}{l}
x^{15} – 15x^{12} – 15x^{10} + 90x^9 – 1350x^7 – 270x^6 + \\
\hphantom{1cm} 75x^5 – 6075x^4 + 405x^3 – 2250x^2 – 2025x – 368 = 0.
\end{array}$$

et c’est un peu long… Pour obtenir des exemples de taille raisonnable, il faut donc être un peu plus astucieux. Une technique qui permet de ne pas augmenter le degré est la suivante. On part d’un nombre $y$ solution d’une équation de degré pas trop grand, par exemple $y = \sqrt[5]{2}$ (qui est solution de l’équation $y^5 = 2$) et on prend pour $x$ un nombre de la forme $x = P(y)$ où $P$ est un polynôme à coefficients entiers. Dans ce cas, $x$ est solution d’une équation de même degré que $y$ qui s’écrit :

$$(x-P(y_1)) (x-P(y_2)) \cdots (x-P(y_d)) = 0$$

où les $y_i$ désignent toutes les solutions complexes de l’équation en $y$ (l’entier $d$ est donc égal au degré de cette équation). Pour notre exemple, on a donc $d = 5$ et les $y_i$ sont les cinq racines cinquièmes complexes de $2$ (avec disons $y_1 = y$). Comme, par définition, $x = P(y)$, il est clair que l’équation donnée ci-dessus est satisfaite ; ce qui est moins évident (mais néanmoins vrai) est que, lorsque l’on développe le membre de gauche de l’équation, les $y_i$ se simplifient tous et on obtient au final une équation en $x$ à coefficients rationnels.

Par cette méthode, si l’on prend encore pour $y$ le nombre $\sqrt[5] 2$ et que l’on choisit pour $P$ le polynôme $2y – y^2 – y^4$, on trouve que $x = 2 \sqrt[5] 2 – \sqrt[5] 4 – \sqrt[5] {16}$ est solution de l’équation $x^5 + 20 x^3 + 140x + 116 = 0$. Ceci est déjà plus satisfaisant.

L’idée à l’origine de la construction de l’exemple du mug est analogue à ce que l’on vient de présenter : on part d’un nombre $y$ auxiliaire qui est solution d’une équation simple et, à partir de lui, on construit un $x$ qui est plus compliqué mais qui reste solution d’une équation de petit degré. Pour le mug, le nombre $y$ auxiliaire considéré est $y = \zeta_{25}$. Il est bien sûr solution de l’équation $y^{25} = 1$ mais, en fait, il est également solution d’une équation simple de degré moindre qui est :

$$y^{20} + y^{15} + y^{10} + y^5 + 1 = 0.$$

Pour le voir, il suffit de remarquer que le membre de gauche est aussi égal à $\frac{y^{25} – 1}{y^5-1}$ (la simplification est possible puisque $y^5 = \zeta_5 \neq 1$). Cette écriture permet également de déterminer les autres solutions de l’équation de degré 20 ci-dessus : ce sont les $y_k = y^k$ pour $k$ variant entre $0$ et $24$ mais $k$ non multiple de $5$.

Le polynôme $P$ choisi dans l’exemple du mug est $P(Y) = Y + Y^7 + Y^{49} + Y^{343}$, les exposants suivant une progression géométrique de raison 7. On a alors :

$$P(y) = y + y^7 + y^{49} + y^{343} = y + y^7 + y^{24} + y^{18}$$

les simplifications provenant du fait que $y^{25} = 1$. On retrouve donc bien $P(y) = x$.

Il s’agit maintenant de trouver l’équation satisfaite et, pour cela, d’après ce que l’on a expliqué précédemment, il suffit de développer le produit des $(x – P(y^k))$ pour $k$ comme précédemment (c’est-à-dire, rappelons-le, variant entre $0$ et $24$ mais en évitant les multiples de $5$). Or, la forme particulière que nous avons choisie pour le polynôme $P$ (avec des exposants en progression géométrique) a une conséquence importante (que l’on laisse en exercice au lecteur) qui est :

pour tout entier $k$ (comme précédemment) [2], $P(y^k) = P(y^{7k})$.

Par ailleurs, bien sûr, comme on l’a déjà utilisé plusieurs fois, du fait que $y^{25} = 1$, on peut toujours ramener les exposants sur $y$ entre $0$ et $24$ : on a $y^{7k} = y^r$ où $r$ désigne le reste de la division euclidienne de $7k$ par $25$.

On déduit de tout cela que, dans le produit des $(x – P(y^k))$ que l’on doit calculer, de nombreux facteurs vont être égaux. Par exemple, le facteur obtenu pour $k = 1$ va être égal à celui obtenu pour $k = 7$, mais aussi à celui obtenu pour $k = 24$ (qui est le reste de la division de $49 = 7 \times 7$ par $25$) et celui obtenu pour $k = 16$ (qui est le reste de la division de $168 = 24 \times 7$ par $25$)… et c’est a priori tout car si l’on continue à multiplier par 7, on tombe sur $126 = 18 \times 7$ qui redonne $1$ après avoir pris le reste dans la division par $25$. De même le facteur correspondant à $k = 2$ est le même que celui correspondant à $k = 14$, et ainsi de suite. Dans le tableau suivant, on a répartit les entiers $k$ que l’on considère en mettant dans une même colonne ceux qui conduisent au même facteur.

$$\begin{array}{|c|c|c|c|c|}
1 & 2 & 3 & 6 & 9 \\
7 & 14 & 21 & 17 & 13 \\
24 & 23 & 22 & 19 & 16 \\
18 & 11 & 4 & 8 & 12
\end{array}$$

On remarquera que chaque ligne du tableau est obtenue à partir de la précédente en multipliant par 7, puis en prenant le reste dans la division euclidienne par 25. En outre, la première ligne s’obtient par la même opération à partir de la dernière.

Au vu du tableau précédent, le produit des $(x – P(y^k))$ que l’on cherche à calculer se réduit à :

$$\big[(x-P(y)) (x-P(y^2)) (x-P(y^3)) (x-P(y^6)) (x-P(y^9)) \big]^4 = 0.$$

Mais, bien entendu, si $x$ est solution de l’équation précédente, il est aussi solution de l’équation dans laquelle on a supprimé la puissance quatrième, ce qui permet de diviser par 4 le degré de l’équation satisfaite par $x$. Après avoir fait cette simplification et avoir développé le produit restant (ce qui demande un peu de patience ou, au choix, l’utilisation d’un logiciel de calcul), on retrouve l’équation proposée sur le mug !

Un peu de théorie de Galois

Pour conclure, expliquons comment on peut trouver une équation algébrique résoluble de degré 5 en utilisant la théorie de Galois. Pour lire la suite, une connaissance de la théorie de Galois est donc requise.

Si $x$ est un nombre complexe, on note $\mathbb Q(x)$ le plus petit sous-corps de $\mathbb C$ contenant l’élément $x$. Si $x$ est algébrique sur $\mathbb Q$ (c’est-à-dire solution d’une équation polynomiale à coefficients rationnels), $\mathbb Q(x)$ est l’ensemble des valeurs prises $P(x)$ lorsque $P$ décrit l’ensemble des polynômes à coefficients rationnels. L’extension $\mathbb Q(x)/\mathbb Q$ est alors finie et son degré est égal au degré du polynôme minimal de $x$.

Commençons par donner l’idée de la construction : pour aboutir à une équation résoluble de degré 5, on va fabriquer une extension de $\mathbb Q$ de degré 5 dont le groupe de Galois est isomorphe à $\mathbb Z/5\mathbb Z$. Or, l’extension cyclotomique $\mathbb Q(\zeta_n)$ — où $\zeta_n$ désigne une racine primitive $n$-ième de l’unité — est galoisienne de groupe de Galois $(\mathbb Z/n\mathbb Z)^\times$ où $(\mathbb Z/n\mathbb Z)^\times$ désigne le groupe des inversibles de l’anneau $(\mathbb Z/n\mathbb Z)$. Par ailleurs, pour $n = 25$, le groupe $\mathbb Z/5\mathbb Z$ apparaît comme un quotient de $(\mathbb Z/25\mathbb Z)^\times$ (car ce dernier groupe s’identifie d’un point de vue abstrait au produit $\mathbb Z/5\mathbb Z \times \mathbb Z/4\mathbb Z$). Il doit donc exister une sous-extension de $\mathbb Q(\zeta_{25})$ de groupe de Galois isomorphe à $\mathbb Z/5\mathbb Z$. Voyons comment on peut la construire explicitement.

Considérons $y = \zeta_{25} \in \mathbb C$ une racine primitive 25-ième de l’unité, par exemple $y = e^{2i\pi/25}$, et posons $K = \mathbb Q(y)$. Le polynôme minimal de $y$ sur $\mathbb Q$ est

$$X^{20} + X^{15} + X^{10} + X^5 + 1 = 0.$$

Ses conjugués (c’est-à-dire les autres racines de son polynôme minimal que l’on vient d’écrire) sont les $y^k$ pour $k$ variant entre 0 et 24 et $k$ non multiple de 5. En particulier, ils sont tous dans $K$, ce qui assure — comme nous l’avons déjà dit — que l’extension $K/\mathbb Q$ est galoisienne. De plus, on a un isomorphisme

$$\varphi : \quad \text{Gal}(K/\mathbb Q) \to (\mathbb Z/25\mathbb Z)^\times$$

qui est défini comme suit : à un élément $\sigma \in \text{Gal}(K/\mathbb Q)$, il associe la classe modulo 25 (qui est uniquement déterminée) d’un entier $k$ tel que $\sigma(y) = y^k$.

En tatonnant un peu, on trouve un sous-groupe de $(\mathbb Z/25\mathbb Z)^\times$ d’ordre 4, par exemple $H = \{1, 7, 16, 24\}$. Ceci nous amène à considérer l’élement $x = y + y^7 + y^{16} + y^{24}$ qui est donc fixe par $G = \varphi^{-1}(H)$. Le corps $K(x)$ est inclus dans le sous-corps de $K(y)$ fixé par $G$, que l’on notera $K(y)^G$. Comme $G$ est d’indice 5 dans $\text{Gal}(K/\mathbb Q)$ (et certainement distingué dans ce groupe car celui-ci est commutatif), l’extension $K(y)^G/\mathbb Q$ est galoisienne de degré 5. Finalement, comme 5 est premier, le corps $K(x)$ qui est coincé entre $\mathbb Q$ et $K(y)^G$ est nécessairement égal à l’un de ces deux corps. Étant donné que $x$ n’est manifestement pas un nombre rationnel, on obtient $K(x) = K(y)^G$.

En conclusion, l’extension $K(x)/\mathbb Q$ est galoisienne de degré 5. Tous les groupes d’ordre 5 étant cyclique, le groupe de Galois de $K(x)/\mathbb Q$ (qui n’est autre que le groupe de Galois de la proposée) est cyclique, isomorphe à $\mathbb Z/5\mathbb Z$. On peut enfin facilement calculer son action sur les racines de la proposée puisque l’on sait que $k \in (\mathbb Z/25\mathbb Z)^\times$ envoie $y$ sur $y^k$ et donc que sa classe modulo $H$ envoie $x = y + y^7 + y^{16} + y^{24}$ sur $y^k + y^{7k} + y^{16k} + y^{24k}$. En revenant aux valeurs $a$, $b$, $c$, $d$, $e$, on trouve les cinq permutations qui apparaissent sur l’image du mug.

On remarquera que, dans la partie précédente, nous avions en fait — sans le savoir — presque calculé le groupe de Galois de la proposée : en tout cas, les colonnes de ce tableau correspondent aux classes (à gauche ou à droite) de $(\mathbb Z/25\mathbb Z)^\times$ suivant $H$ (ou, via $\varphi$ aux classes de $\text{Gal}(K(x)/\mathbb Q)$ suivant $G$), c’est-à-dire aux éléments du groupe de Galois de l’équation qui nous intéresse. Un très bon exercice pour le lecteur est d’essayer d’expliquer le mieux possible cette « coïncidence ».

Notes

[1] On dispose malgré tout, pour ce faire, de méthodes systématiques qui reposent, par exemple, sur le calcul de résultants.

[2] On mentionne « comme précédemment » entre parenthèses car la propriété donnée ne sera utilisée dans la suite que pour ces $k$-là. Toutefois, elle reste vraie pour tout entier $k$.