par M. Coste
Cet article est publié simultanément sur le site de la revue Images des mathématiques. Nous remercions en particulier l’auteur d’avoir permis cette collaboration.
Le jeu de taquin et le problème de Sam Loyd
Vous connaissez peut-être déjà le jeu de taquin. Ce jeu se compose d’un cadre contenant quinze plaques carrées numérotées de 1 à 15, laissant un espace dans lequel on peut faire coulisser une plaque voisine.
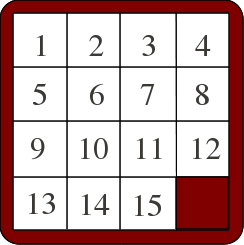
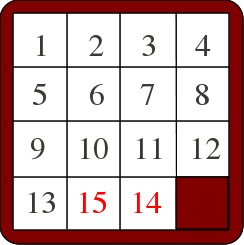
Un casse-tête posé par Sam Loyd, il y a plus d’un siècle, a fait couler pas mal d’encre : peut-on, par une suite de mouvement autorisés du taquin (l’usage d’un manche de petite cuillère pour démonter le taquin est formellement interdit), passer de la position initiale à la position qui en diffère seulement par l’interversion des cases numérotées 14 et 15 ?

Pour répondre au petit casse-tête de Sam Loyd, nous allons étudier comment les configurations du taquin changent par les mouvements autorisés. Il sera plus facile de travailler avec des nombres disposés à la queue-leu-leu plutôt que rangés dans un tableau. Voici comment nous rangeons les nombres: à une position du taquin, on associe la liste des numéros que l’on rencontre en parcourant les cases le long du chemin indiqué ci-dessous. On ne tient pas compte de la case vide. Le chemin vert ressemble à une file d’attente aux guichets d’une gare, entre des barrières qui zigzaguent, n’est-ce pas ?
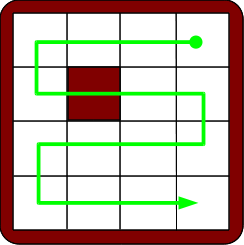
On obtient ainsi un rangement des nombres de 1 à 15. Par exemple, le rangement associé à la configuration de départ du taquin est
| 4 | 3 | 2 | 1 | 5 | 6 | 7 | 8 | 12 | 11 | 10 | 9 | 13 | 14 | 15 |
Le rangement des nombres de 1 à 15 ne détermine pas complètement la configuration du taquin, car il ne donne pas d’information sur la position de la case vide. Mais comme on peut promener la case vide le long du chemin par les mouvements autorisés du taquin, peu importe: si l’on peut arriver à l’une des configurations donnant un certain rangement, on pourra aussi arriver à toutes les configurations donnant le même rangement.
Nombre d’inversions
Nous allons mesurer le « dérangement » d’un rangement R donné des nombres de 1 à 15 (ou de 1 à un entier quelconque) par rapport au rangement par ordre croissant. On dira qu’une paire de nombres présente une inversion dans le rangement R si le plus grand des deux nombres vient avant le plus petit dans R. Par exemple, dans le rangement suivant des nombres de 1 à 9
| 9 | 2 | 5 | 4 | 1 | 6 | 8 | 3 | 7 |
la paire 3,5 présente une inversion, mais la paire 4,6 ne présente pas d’inversion. Combien y a-t-il d’inversions en tout dans le rangement ci-dessus ? Ce n’est pas évident de compter sans se tromper. Alors, voici une méthode. On commence par les paires avec 1 : le nombre 1, qui est le plus petit, présente une inversion avec tous les nombres qui sont rangés avant lui. Ça fait quatre inversions (avec 9, 2, 5 et 4). Effaçons 1.
| 9 | 2 | 5 | 4 | 6 | 8 | 3 | 7 |
Maintenant 2 est le plus petit des nombres restants, et il présente une inversion avec tous les nombres rangés avant lui. Ce qui fait juste une inversion (avec 9). Vous voyez comment continuer ? On efface 2 et on compte les nombres avant 3, on efface 3 et on compte les nombres avant 4 etc. (pour faciliter le décompte, les « nombres avant » sont soulignés dans le tableau ci-dessous).
| 9 | 5 | 4 | 6 | 8 | 3 | 7 | ||
| 9 | 5 | 4 | 6 | 8 | 7 | |||
| 9 | 5 | 6 | 8 | 7 | ||||
| 9 | 6 | 8 | 7 | |||||
| 9 | 8 | 7 | ||||||
| 9 | 8 | |||||||
| 9 |
Voila, au total 17 inversions. Armés de la méthode que nous venons de décrire, nous pouvons trouver sans erreur le nombre d’inversions du rangement des nombres de 1 à 15 associé à la configuration de départ du taquin. Vous trouvez bien 12 ? Nous nous sommes donnés beaucoup de peine pour calculer le nombre d’inversions mais, en fait, la seule chose qui va nous intéresser dans la suite est de savoir si ce nombre d’inversions est pair ou impair.
Sauts-de-moutons
Si on part d’un rangement des nombres de 1 à 15, par quelles opérations peut-on remettre les nombres dans l’ordre croissant ? En fait, il suffit d’utiliser des
« sauts-de-moutons » : un saut-de-mouton consiste à faire sauter un nombre qui n’est pas à la première place du rangement par-dessus celui qui le précède. Par exemple, avec une situation où il n’y a que les nombres de 1 à 4 :
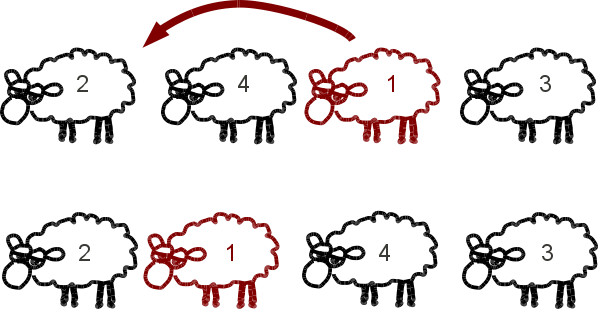
On voit aisément une façon de remettre les nombres dans l’ordre croissant en utilisant des sauts-de-moutons : amener le 1 à la première place, s’il n’y est pas déjà, par des sauts-de-moutons, puis amener le 2 à la deuxième place etc. Sur l’exemple ci-dessus, le mouton qui saute par dessus celui qui le précède est indiqué en rouge :
| 2 | 4 | 1 | 3 |
| 2 | 1 | 4 | 3 |
| 1 | 2 | 4 | 3 |
| 1 | 2 | 4 | 3 |
La lectrice attentive aura sans doute remarqué que, par ce procédé, le nombre de sauts-de-mouton utilisés pour remettre les nombres dans l’ordre croissant (trois sauts de mouton, dans l’exemple) est précisément égal au nombre d’inversions du rangement de départ. Mais on pourrait imaginer d’autres façons de procéder, par exemple :
| 2 | 4 | 1 | 3 |
| 2 | 4 | 3 | 1 |
| 2 | 3 | 4 | 1 |
| 2 | 3 | 1 | 4 |
| 2 | 1 | 3 | 4 |
| 1 | 2 | 3 | 4 |
Cette fois-ci, on a procédé en cinq sauts-de-moutons. Aurait-on pu le faire en quatre sauts-de-moutons ? Pour répondre à cette question, examinons comment change le nombre d’inversions du rangement à chaque saut-de-mouton. Puisqu’un saut-de-mouton ne fait qu’échanger les places de deux nombres voisins, il diminue de un le nombre d’inversions si ces deux nombres étaient rangés dans le mauvais ordre au départ, et il l’augmente de un s’ils étaient rangés dans le bon ordre. Dans les deux cas, le nombre d’inversions a changé de parité : s’il était pair, il est devenu impair, et vice-versa. Donc, pour passer du rangement 2, 4, 1, 3 de départ (où le nombre d’inversions est trois, un nombre impair) au rangement dans l’ordre croissant (c.-à-d. le rangement pour lequel le nombre d’inversions est zéro, un nombre pair), il faut nécessairement faire un nombre impair de sauts-de-moutons. On ne peut pas le faire en quatre sauts-de-moutons. Retenons bien ce qui nous a servi :
chaque saut-de-mouton change la parité du nombre d’inversions.
La solution du problème de Sam Loyd
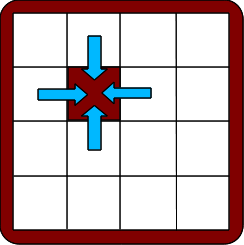
Un mouvement autorisé du jeu de taquin modifie le rangement des nombres de 1 à 15 que nous avons associé à la configuration, si le déplacement de la case vide ne se fait pas le long du chemin vert décrit plus haut. Par exemple, que se passe-t-il si on effectue les mouvements indiqués ci-dessous ?
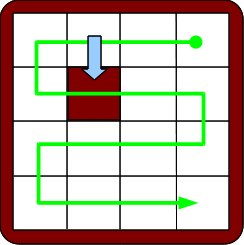
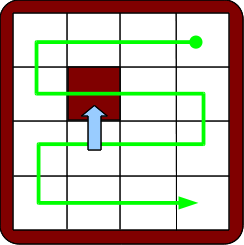
Le mouvement de gauche fait reculer le nombre porté par la case qui bouge de deux places dans la file d’attente. Ceci peut se faire par deux sauts-de-moutons dans le rangement des nombres. Le mouvement de droite fait avancer le nombre porté par la case qui bouge de quatre places dans la file. Ceci peut se faire par quatre sauts-de-moutons. Dans les deux cas, le nombre de sauts-de-moutons effectués est pair, et donc la parité du nombre d’inversions ne change pas. On se convainc facilement qu’il en est de même pour tous les mouvements autorisés du taquin : s’ils changent le rangement, c’est en faisant avancer ou reculer un nombre de deux, quatre ou six places dans la liste.
Un mouvement autorisé du taquin ne change pas la parité du nombre d’inversions
Revenons maintenant au problème de Sam Loyd. On peut passer du rangement des nombres associé à la configuration de départ à celui où 14 et 15 sont échangés par un seul saut-de-mouton. Donc les parités des nombres d’inversions des deux rangements sont différentes. Et ceci montre qu’on ne peut pas passer de la configuration de départ à la configuration où 14 et 15 sont échangés par une suite de mouvements autorisés du taquin, puisque ceux-ci conservent la parité du nombre d’inversions.
Il est impossible d’arriver à la configuration demandée par Sam Loyd en n’utilisant que les mouvements autorisés du taquin
Pourquoi Galois ?
Quel rapport entre Évariste Galois et le taquin ? En fait, l’outil que nous avons utilisé, à savoir les rangements des nombres de 1 à 15, s’appelle en termes plus savants les permutations de l’ensemble {1,2,…,15}. Les permutations occupent une place centrale de l’œuvre de Galois : c’est en étudiant les permutations de l’ensemble des racines d’une équation qu’il a pu établir que les racines d’une équation de degré supérieur ou égal à 5 ne peuvent pas en général se trouver en utilisant des radicaux.
Les sauts-de-moutons qui nous ont été si utiles sont des exemples de transpositions (les transpositions sont des permutations qui ne font qu’échanger deux éléments de l’ensemble). Ce que nous avons montré chemin faisant, à savoir qu’on peut remettre dans l’ordre croissant les nombres de n’importe quel rangement en utilisant uniquement des sauts-de-moutons, s’énonce comme le théorème mathématique suivant: les transpositions de deux nombres successifs engendrent le groupe des permutations de {1,…,n}.
L’argument clé pour démontrer l’impossibilité du casse-tête de Sam Loyd a été l’invariance de la parité du nombre d’inversions. La parité du nombre d’inversions est ce que les mathématiciens appellent la signature d’une permutation. Et ce que nous avons vu en utilisant les sauts-de-moutons est une démonstration du théorème qui dit que la signature est l’unique homomorphisme non trivial du groupe des permutations de {1,…,n} dans le groupe Z/2Z. C’est plus impressionnant dit comme ça, n’est-ce-pas ?
Pour en revenir à Galois, vous pouvez voir ci-dessous une page extraite d’un de ses mémoires. Galois y considère des groupes de permutations des quatre lettres a,b,c,d représentant les racines d’un polynôme de degré quatre. Il explique comment la résolution d’une telle équation par radicaux correspond à un emboîtement de tels groupes de permutations de plus en plus petits. De manière générale, la résolubilité d’une équation par radicaux correspond à la possibilité de réaliser de tels emboîtements de groupes de permutations.

Et après ?
La résolution du problème de Sam Loyd n’épuise pas les questions que l’on peut se poser à propos du jeu de taquin. Une question qui vient naturellement est la suivante. Nous avons vu qu’une configuration que l’on peut obtenir par des mouvements autorisés du taquin vérifie obligatoirement l’invariance de la parité du nombre d’inversions (de la signature, suivant la terminologie mathématique). Mais, dans l’autre sens, est-ce qu’une configuration vérifiant l’invariance de la signature peut toujours être obtenue par des mouvements autorisés du taquin ? On peut voir la réponse (positive !) à cette question, rédigée dans un langage mathématique assez sophistiqué, dans le texte disponible ici.
Une autre question, sans doute plus facile que la précédente : que se passe-t-il si on remplace le cadre de 4×4 cases par un cadre de $1811\times 2011$ cases, avec $(1811\times 2011)-1 = 3641920$ plaques numérotées ? Le problème de Sam Loyd (l’échange des plaques numérotées 3641919 et 3641920) pourrait-il avoir une solution pour ce gigantesque taquin où on a plus de liberté de mouvement ?
Lors du colloque et de l’après-midi grand public, nous vous avons distribué un taquin non standard, auquel vous pouvez également jouer de manière interactive sur ce site (attention, la règle du jeu se mélange également lorsque l’on clique sur le bouton « Mélange » !). Il s’analyse de la même manière que le taquin présenté dans cet article : peu importe au fond ce qui est écrit sur les plaques, du moment qu’on peut les différencier. La spécialité de ce nouveau taquin est qu’il n’est pas possible (sans démonter le taquin) d’échanger les chiffres rouges avec les chiffres verts. Sauriez-vous le démontrer ?
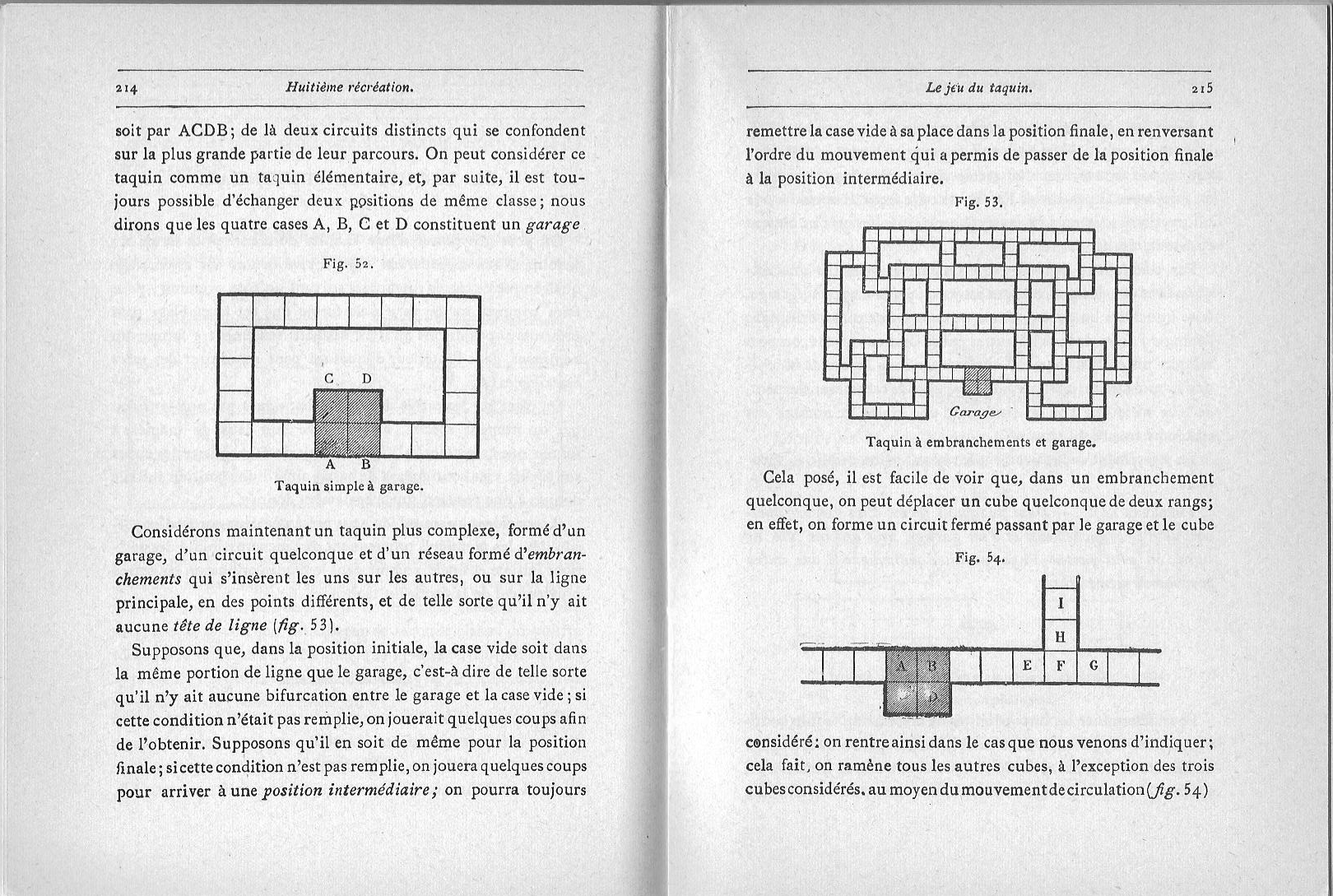
On peut lire beaucoup de choses intéressantes autour du taquin dans le chapitre du livre d’Édouard Lucas (Récréations mathématiques, vol. 1, Gauthier-Villars 1882 — nouveau tirage, Blanchard 1960) consacré à ce jeu. Ci-dessous, vous pouvez constater que Lucas considère même des « taquins à embranchements et garage » !
 English
English  Français
Français 

